2. (2024春·仪征期末)在综合与实践课上,老师让同学们以“三角板与平行线”为主题开展数学活动。已知直线$AB$,$CD$,$AB// CD$,在直角三角板$EFG$中,$\angle FEG= 90^{\circ}$,$\angle EGF= 60^{\circ}$。
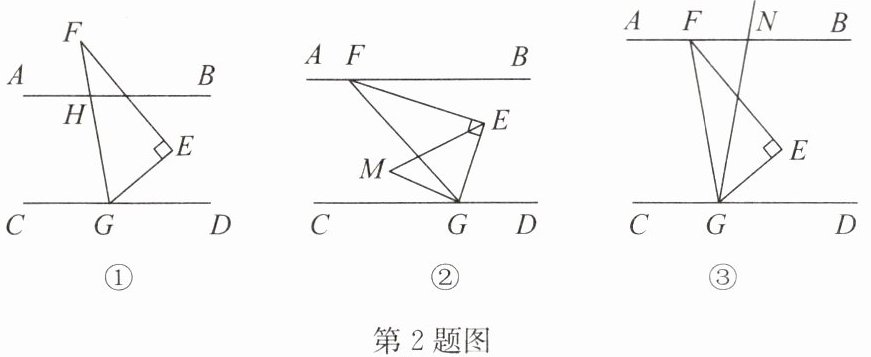
(1)小明将三角板按如图①方式摆放,点$G在CD$上,边$GF与AB交于点H$,若$\angle FHA= 80^{\circ}$,则$\angle EGD$的度数是______;
(2)小亮将三角板按如图②方式摆放,点$F$,$G分别在AB$,$CD$上,$\angle FEG的平分线与\angle FGC的平分线交于点M$,若$\angle EGD= 4\angle BFE$,求$\angle M$的度数;
(3)小颖将图②中的三角板进行适当转动,点$F$,$G仍然分别在AB$,$CD$上,如图③,再将$\angle DGE沿边GE$翻折,边$GD的对应边GN与AB交于点N$,小颖给出下列两个结论:
①$\angle CGN+\angle BFE$的值不变;②$\frac{\angle CGN}{\angle BFE}$的值不变。
其中只有一个是正确的,你认为哪个是正确的?请说明理由。
答案:2. (1)$40^{\circ}$ 点拨:∵$\angle FHA = 80^{\circ}$,$AB // CD$,
∴$\angle CGH = \angle AHF = 80^{\circ}$.
∵$\angle FGE = 60^{\circ}$,∴$\angle EGD = 180^{\circ} - 60^{\circ} - 80^{\circ} = 40^{\circ}$.
(2)解:如答图,过点$E$作$EK // AB$.

∵$AB // CD$,∴$AB // EK // CD$,
∴$\angle BFE = \angle KEF$,$\angle KEG = \angle EGD$.
∵$\angle FEK + \angle KEG = \angle FEG = 90^{\circ}$,
∴$\angle BFE + \angle EGD = 90^{\circ}$.
∵$\angle EGD = 4\angle BFE$,
∴$\angle BFE = 18^{\circ}$,$\angle EGD = 72^{\circ}$.
∵$\angle FGE = 60^{\circ}$,∴$\angle FGC = 180^{\circ} - 60^{\circ} - 72^{\circ} = 48^{\circ}$.
∵$EM$平分$\angle FEG$,$GM$平分$\angle FGC$,
∴$\angle FEM = \frac{1}{2} × 90^{\circ} = 45^{\circ}$,$\angle MGC = \frac{1}{2} × 48^{\circ} = 24^{\circ}$,
∴$\angle KEM = 45^{\circ} - 18^{\circ} = 27^{\circ}$,
同理可得:$\angle M = \angle KEM + \angle MGC = 27^{\circ} + 24^{\circ} = 51^{\circ}$.
(3)解:②$\frac{\angle CGN}{\angle BFE}$的值不变是正确的.理由如下:
设$\angle DGE = \angle NGE = x^{\circ}$,∴$\angle CGN = 180^{\circ} - 2x^{\circ}$.
同理可得:$\angle BFE + \angle DGE = \angle FEG = 90^{\circ}$,
∴$\angle BFE = 90^{\circ} - x^{\circ}$,
∴$\frac{\angle CGN}{\angle BFE} = \frac{180^{\circ} - 2x^{\circ}}{90^{\circ} - x^{\circ}} = 2$,
$\angle CGN + \angle BFE = 180^{\circ} - 2x^{\circ} + 90^{\circ} - x^{\circ} = 270^{\circ} - 3x^{\circ}$,
∴①$\angle CGN + \angle BFE$的值变化,②$\frac{\angle CGN}{\angle BFE}$的值不变.