1. 已知实数$a,b满足a^{2}+b^{2}= 3+ab$,则$(2a - 3b)^{2}+(a + 2b)(a - 2b)$的最大值为
22
。
答案:22 点拨:$\because a^{2}+b^{2}=3+ab,$
$\therefore (2a-3b)^{2}+(a+2b)(a-2b)$
$=4a^{2}+9b^{2}-12ab+a^{2}-4b^{2}$
$=5a^{2}+5b^{2}-12ab$
$=5(a^{2}+b^{2})-12ab$
$=15+5ab-12ab$
$=15-7ab,$
$\because a^{2}+b^{2}=3+ab,\therefore (a+b)^{2}=3+3ab,$
$\therefore ab=\frac {1}{3}(a+b)^{2}-1,\therefore ab$的最小值为-1,
$\therefore -7ab$的最大值为 7,
$\therefore (2a-3b)^{2}+(a+2b)(a-2b)$的最大值为 22.
2. 已知$m - n = 4,mn = - 3$,求$(m^{2}-4)(n^{2}-4)$的值。
答案:解:$\because m-n=4,mn=-3,\therefore m^{2}+n^{2}=(m-n)^{2}+2mn=$
$4^{2}+2×(-3)=16-6=10.$
$(m^{2}-4)(n^{2}-4)=(mn)^{2}-4(m^{2}+n^{2})+16,$
当$mn=-3,m^{2}+n^{2}=10$时,
原式$=(-3)^{2}-4×10+16=9-40+16=-15.$
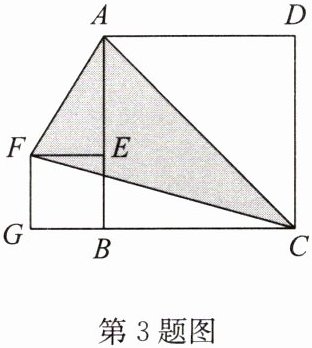
3. 如图,正方形$ABCD的边长为a$,点$E在AB$边上,四边形$EFGB$也是正方形,它的边长为$b(a>b)$,连接$AF,CF,AC$。
(1)用含$a,b的代数式表示GC= $
$a+b$
;
(2)若两个正方形的面积之和为60,即$a^{2}+b^{2}= 60$,又$ab = 20$,求线段$GC$的长;
解:$\because (a+b)^{2}=a^{2}+b^{2}+2ab=60+20×2=100,$
$\therefore a+b=10,\therefore GC=10.$
(3)若$a = 8$,$\triangle AFC的面积为S$,则$S= $
32
。
答案:(1)$a+b$
(2)解:$\because (a+b)^{2}=a^{2}+b^{2}+2ab=60+20×2=100,$
$\therefore a+b=10,\therefore GC=10.$
(3)32 点拨:$S=S_{\triangle AFC}=S_{\triangle AFE}+S_{正方形FGBE}+S_{\triangle ABC}-S_{\triangle FGC}$
$=\frac {1}{2}b(a-b)+b^{2}+\frac {1}{2}a^{2}-\frac {1}{2}b(b+a)$
$=\frac {1}{2}ab-\frac {1}{2}b^{2}+b^{2}+\frac {1}{2}a^{2}-\frac {1}{2}b^{2}-\frac {1}{2}ab$
$=\frac {1}{2}a^{2}$
$=\frac {1}{2}×8^{2}$
$=32.$