2025年启东中学作业本八年级数学上册人教版第23页解析答案

1. (2024·黑龙江二模)如图,在边长为2的等边三角形ABC中,D是BC的中点,点E在线段AD上,连接BE,在BE的下方作等边三角形BEF,连接DF,则△BDF周长的最小值为______。

答案：
$\sqrt{3}+1$ 点拨：$\because \triangle ABC$ 是等边三角形，$D$ 是 $BC$ 的中点，$\therefore \angle BAD = 30^{\circ}, BD = \frac{1}{2}BC = 1$.
如答图，作射线 $CF$.

$\because \triangle ABC,\triangle BEF$ 都是等边三角形，$\therefore AB = BC = AC, BE = EF = BF, \angle BAC = \angle ABC = \angle ACB = \angle EBF = \angle BEF = \angle BFE = 60^{\circ}$，$\therefore \angle ABC - \angle EBD = \angle EBF - \angle EBD$，$\therefore \angle ABE = \angle CBF$，$\therefore \triangle BAE \cong \triangle BCF(SAS), \therefore \angle BCF = \angle BAD = 30^{\circ}$，$\therefore$ 射线 $CF$ 与 $CB$ 的夹角始终成 $30^{\circ}$.
如答图，作点 $D$ 关于 $CF$ 的对称点 $G$，连接 $CG,DG,FG,BG$，则 $FD = FG, CD = CG$，$\therefore \triangle BDF$ 的周长 $= FB + FD + BD = FB + FG + 1 \geqslant BG + 1$，$\therefore \triangle BDF$ 的周长的最小值为 $BG + 1$.
由轴对称的性质，可得 $\angle DCG = 2\angle BCF = 60^{\circ}$，$\therefore \triangle DCG$ 是等边三角形，$\therefore DG = DC = DB, \angle CDG = 60^{\circ}$，$\therefore \angle BGD = \angle GBD = \frac{1}{2}\angle CDG = 30^{\circ}$，$\therefore \angle CGB = \angle CGD + \angle DGB = 90^{\circ}$.
在 $Rt\triangle CBG$ 中，$BC = 2, CG = CD = 1, \therefore BG = \sqrt{3}$，$\therefore \triangle BDF$ 周长的最小值是 $\sqrt{3}+1$.

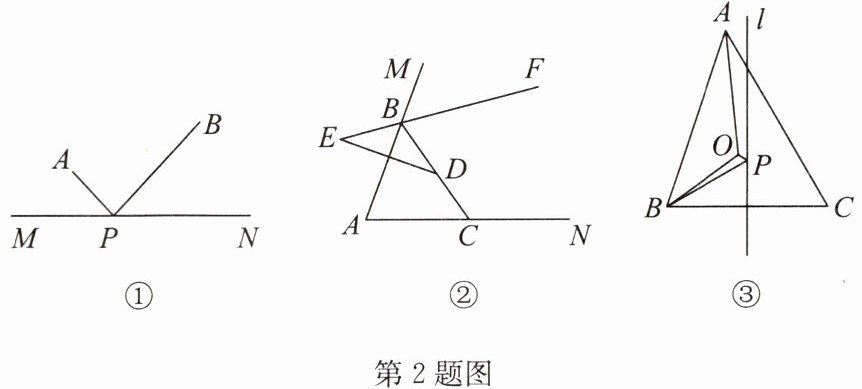
2. 【了解概念】如图①,已知A,B为直线MN同侧的两点,P为直线MN上的一点,连接AP,BP,若∠APM= ∠BPN,则称点P为点A,B关于直线MN的“等角点”。
【理解运用】(1)如图②,在△ABC中,D为BC上一点,点D,E关于直线AB对称,连接EB并延长至点F,判断点B是否为点D,F关于直线AB的“等角点”,并说明理由；
【拓展提升】(2)如图②,在(1)的条件下,若∠A= 70°,AB= AC,Q是射线EF上一点,且点D,Q关于直线AC的“等角点”为点C,请利用尺规在图②中确定点Q的位置,并求出∠BQC的度数；
(3)如图③,在△ABC中,∠ABC,∠BAC的平分线交于点O,点O到AC的距离为1,直线l垂直平分边BC,点P为点O,B关于直线l的“等角点”,连接OP,BP,当∠ACB= 60°时,OP+BP的值为______。

答案：
(1) 解：点 $B$ 是点 $D,F$ 关于直线 $AB$ 的“等角点”. 理由如下：
$\because$ 点 $D,E$ 关于直线 $AB$ 对称，$\therefore BE = BD, AB \perp DE$，$\therefore \angle ABE = \angle ABC$；$\because \angle ABE = \angle MBF$，$\therefore \angle ABC = \angle MBF$，$\therefore$ 点 $B$ 是点 $D,F$ 关于直线 $AB$ 的“等角点”.
(2) 解：如答图①，点 $Q$ 即为所求.
$\because \angle A = 70^{\circ}, AB = AC, \therefore \angle ABC = \angle ACB = 55^{\circ}$.
$\because$ 点 $D,Q$ 关于直线 $AB,AC$ 的“等角点”分别为点 $B$ 和点 $C$，$\therefore \angle MBQ = \angle NCQ = 55^{\circ}$，$\therefore \angle CBQ = \angle BCQ = 70^{\circ}, \therefore \angle BQC = 40^{\circ}$.

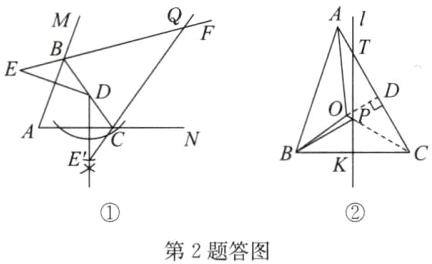
(3) 2 点拨：如答图②，直线 $l$ 交 $AC$ 于点 $T$，作 $OD \perp AC$ 于点 $D$，连接 $PC,OC$.
$\because$ 直线 $l$ 垂直平分边 $BC$，$\therefore PB = PC$，$\therefore \angle BPK = \angle CPK$.
$\because$ 点 $P$ 为点 $O,B$ 关于直线 $l$ 的“等角点”，$\therefore \angle OPT = \angle BPK$，$\therefore \angle CPK = \angle OPT$，$\therefore O,P,C$ 三点共线，$\therefore OP + BP = OP + PC = OC$.
$\because AO$ 平分 $\angle BAC, BO$ 平分 $\angle ABC$，$\therefore \angle OCD = \frac{1}{2}\angle ACB = 30^{\circ}$，$\therefore OC = 2OD = 2$，$\therefore$ 此时 $OP + BP = 2$.