2025年启东中学作业本八年级数学上册人教版第22页解析答案

1. (2023秋·东城区期末)如图,在Rt△ABC中,∠ACB= 90°,∠ABC= 30°,AC= 6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,当CF取最小值时,△BDE的周长为______.

答案：
18 点拨: 如答图，连接 BF，过点 C 作 CH⊥BF，交 BF 的延长线于点 H，交 AB 于点 D'。
　　　　　　　

∵△BDE 是等边三角形，F 是 DE 的中点，
∴∠ABF = 30°，
∴点 F 在射线 BF 上运动，
∴当点 F 与点 H 重合时，CF 最小。
∵∠ACB = 90°，∠ABC = 30°，
∴∠A = 60°，AB = 2AC = 12。
∵∠ABF = 30°，
∴∠BD'H = ∠AD'C = 60°，
∴△ACD'是等边三角形，
∴AD' = AC = 6，
∴BD' = AB - AD' = 12 - 6 = 6，
∴当 CF 取最小值时，△BDE 的周长为 3×6 = 18。

2. 如图,在△ABC中,AB= AC= 8,∠C= 30°,D是BC边上的一个动点,连接AD,以AD为边作△ADE,使AD= AE,∠AED= ∠C.O为AC的中点,连接OE,则线段OE的最小值为______.

答案：
2 点拨: 如答图，取 AB 的中点 G，连接 DG，CG。
　　　　　　　

∵AB = AC = 8，O 是 AC 的中点，G 是 AB 的中点，
∴AG = BG = AO = CO = 4。
∵AB = AC，∠AED = ∠ACB，∠ACB = 30°，
∴∠B = ∠ACB = 30°，∠AED = ∠ACB = 30°，
∴∠BAC = ∠DAE = 120°，∴∠BAD = ∠CAE。
在△ADG 和△AEO 中，{AD = AE，∠GAD = ∠OAE，AG = AO}
∴△ADG ≌ △AEO(SAS)，∴GD = EO，
∴DG 有最小值时，EO 也有最小值。
∴当 GD⊥BC 时，GD 有最小值。
∵∠B = 30°，GD⊥BC，BG = 4，∴GD = 2，
∴线段 OE 的最小值为 2。

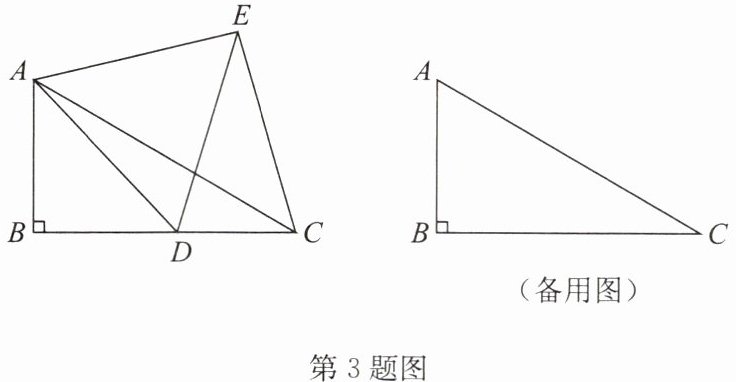
3. 如图,在Rt△ABC中,∠B= 90°,∠ACB= 30°,BC= $\sqrt{3}$,点D在边BC上,连接AD,在AD的右侧作等边三角形ADE,连接EC.
(1)求证：DE= CE；
(2)若点D在BC的延长线上,其他条件不变,直接写出DE,CE之间的数量关系(不必证明)；
(3)当点D从点B出发沿着线段BC运动到点C时,求点E的运动路径长.

答案：
(1) 证明: 如答图①，取 AC 的中点 F，连接 EF，则 AF = $\frac{1}{2}$AC。
∵在 Rt△ABC 中，∠ACB = 30°，
∴AB = $\frac{1}{2}$AC，∠BAC = 60°，∴AB = AF。
∵△ADE 是等边三角形，∴∠DAE = 60°，AD = AE = DE，
∴∠BAD + ∠DAC = ∠DAC + ∠CAE = 60°，
∴∠BAD = ∠FAE，
∴△ABD ≌ △AFE(SAS)，∴∠AFE = ∠B = 90°，
∴EF 垂直平分 AC，∴AE = CE，∴DE = CE。
　

(2) 解: DE = CE。
(3) 解: 如答图②。
当点 D 与点 B 重合时，点 E 在点 E'处，此时 E'是 AC 的中点。
当点 D 与点 C 重合时，点 E 在点 E''处，此时△ACE''是等边三角形，由(1)得 AE'' = CE''，
∴点 E 始终落在线段 AC 的垂直平分线上，
∴E'E''垂直平分 AC，
∴点 E 的运动路径是从 AC 的中点 E'，沿着 AC 的垂直平分线运动到点 E''。
由(1)得 AE' = AB，AE'' = AC，
∴Rt△E'AE'' ≌ Rt△BAC(HL)，∴E'E'' = BC = $\sqrt{3}$，
∴点 E 的运动路径长为 $\sqrt{3}$。