18. 如图,在$\triangle ABC$中,$AB= 6$,$AC= 5$,$BC= 9$,$∠BAC的平分线AP交BC于点P$,则$CP$的长为
$\frac{45}{11}$
.
答案:$\frac{45}{11}$
解析:
解:∵AP是∠BAC的平分线,
∴由角平分线定理得:$\frac{BP}{CP}=\frac{AB}{AC}$。
∵AB=6,AC=5,
∴$\frac{BP}{CP}=\frac{6}{5}$。
设CP=x,则BP=$\frac{6}{5}x$。
∵BC=9,BP+CP=BC,
∴$\frac{6}{5}x + x = 9$。
解得$x=\frac{45}{11}$。
即CP的长为$\frac{45}{11}$。
19. (6分)如图,$AB// CD$,$AB= CD$,$CE= BF$. 求证:$AE// DF$.
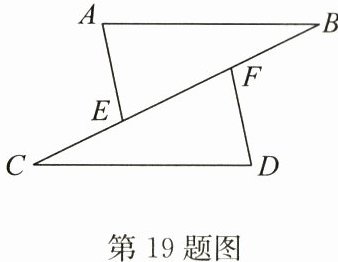
答案:证明:$\because AB// CD,\therefore \angle B=\angle C$.
$\because CE=BF,\therefore CF=BE$.
在$\triangle ABE$与$\triangle DCF$中,$\left\{\begin{array}{l} AB=DC,\\ \angle B=\angle C,\\ BE=CF,\end{array}\right.$
$\therefore \triangle ABE\cong \triangle DCF(SAS)$,
$\therefore \angle AEB=\angle DFC,\therefore AE// DF$.
20. (6分)如图,点$C在线段BD$上,在$\triangle ABC和\triangle DEC$中,$∠A= ∠D$,$AB= DE$,$∠B= ∠E$. 求证:$AC= DC$.

答案:证明:在$\triangle ABC$和$\triangle DEC$中,
$\left\{\begin{array}{l} \angle A=\angle D,\\ AB=DE,\\ \angle B=\angle E,\end{array}\right.$ $\therefore \triangle ABC\cong \triangle DEC(ASA),\therefore AC=DC$.
21. (6分)如图,点$C在线段AB$上,$CF平分∠DCE$,$AD// EB$,$∠ADC= ∠BCE$,$AD= BC$. 求证:$DF= EF$.

答案:证明:$\because AD// BE,\therefore \angle DAC=\angle CBE$.
在$\triangle ACD$和$\triangle BEC$中,$\left\{\begin{array}{l} \angle ADC=\angle BCE,\\ AD=BC,\\ \angle DAC=\angle CBE,\end{array}\right.$
$\therefore \triangle ACD\cong \triangle BEC,\therefore DC=CE$.
$\because CF$平分$\angle DCE,\therefore \angle DCF=\angle ECF$.
在$\triangle DCF$和$\triangle ECF$中,$\left\{\begin{array}{l} DC=EC,\\ \angle DCF=\angle ECF,\\ CF=CF,\end{array}\right.$
$\therefore \triangle DCF\cong \triangle ECF,\therefore DF=EF$.
22. (8分)如图,$BE\perp AC于点E$,$CF\perp AB于点F$,$BE与CF交于点D$,$DE= DF$,连接$AD$.
求证:(1)$∠FAD= ∠EAD$;
(2)$BD= CD$.

答案:证明:(1)$\because BE\perp AC,CF\perp AB,DE=DF$,
$\therefore AD$是$\angle BAC$的平分线,$\therefore \angle FAD=\angle EAD$.
(2)$\because BE\perp AC,CF\perp AB,\therefore \angle DEA=\angle DFA=90^{\circ}$.
在$Rt\triangle ADF$和$Rt\triangle ADE$中,$\left\{\begin{array}{l} AD=AD,\\ DF=DE,\end{array}\right.$
$\therefore Rt\triangle ADF\cong Rt\triangle ADE(HL),\therefore \angle ADF=\angle ADE$.
$\because \angle BDF=\angle CDE,\therefore \angle ADF+\angle BDF=\angle ADE+\angle CDE$,即$\angle ADB=\angle ADC$.
在$\triangle ABD$和$\triangle ACD$中,$\left\{\begin{array}{l} \angle BAD=\angle CAD,\\ AD=AD,\\ \angle ADB=\angle ADC,\end{array}\right.$
$\therefore \triangle ABD\cong \triangle ACD(ASA),\therefore BD=CD$.