9. 如图,$AD是\triangle ABC$的中线,$CE是AB$边上的高,$AB= 4$,$S_{\triangle ADC}= 6$,则$CE= $(
D
)
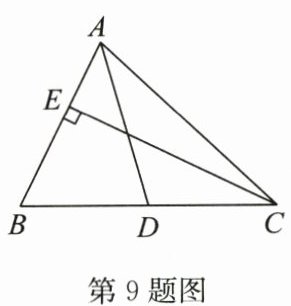
A.3
B.4
C.5
D.6
答案:D
解析:
解:∵AD是△ABC的中线,
∴BD=DC,
∵S△ADC=6,
∴S△ABD=S△ADC=6,
∴S△ABC=S△ABD+S△ADC=12,
∵CE是AB边上的高,AB=4,
∴S△ABC=$\frac{1}{2}$·AB·CE,
即12=$\frac{1}{2}$×4×CE,
解得CE=6。
答案:D
10. 三角形中,如果一个角是另一个角的3倍,这样的三角形我们称为“灵动三角形”.例如,三个内角分别为$120^{\circ },40^{\circ },20^{\circ }$的三角形是“灵动三角形”.如图,$∠MON= 60^{\circ }$,在射线$OM上找一点A$,过点$A作AB⊥OM交ON于点B$,以点$A为端点作射线AD$,交线段$OB于点C$(规定$0^{\circ }<∠OAC<90^{\circ }$).有下列结论:①$∠ABO的度数为30^{\circ }$;②$\triangle AOB$是“灵动三角形”;③若$∠BAC= 70^{\circ }$,则$\triangle AOC$是“灵动三角形”;④当$\triangle ABC$是“灵动三角形”时,$∠OAC为30^{\circ }或52.5^{\circ }$.其中正确结论的个数是(
C
)
A.1
B.2
C.3
D.4
答案:C
解析:
解:①∵AB⊥OM,∴∠OAB=90°,∵∠MON=60°,∴∠ABO=180°-90°-60°=30°,①正确。
②∠OAB=90°,∠MON=60°,∠ABO=30°,90°=3×30°,∴△AOB是“灵动三角形”,②正确。
③∠BAC=70°,∠OAB=90°,∴∠OAC=90°-70°=20°,∠AOC=60°,∠ACO=180°-60°-20°=100°,100°不是60°或20°的3倍,60°不是20°的3倍,∴△AOC不是“灵动三角形”,③错误。
④设∠OAC=α,则∠BAC=90°-α,∠ABC=30°,∠ACB=180°-30°-(90°-α)=60°+α。
情况1:∠ABC=3∠BAC,30°=3(90°-α),α=80°(舍,0°<α<90°但此时∠ACB=140°,不满足);
情况2:∠BAC=3∠ABC,90°-α=3×30°,α=0°(舍);
情况3:∠ACB=3∠ABC,60°+α=3×30°,α=30°;
情况4:∠ABC=3∠ACB,30°=3(60°+α),α=-50°(舍);
情况5:∠ACB=3∠BAC,60°+α=3(90°-α),α=52.5°;
情况6:∠BAC=3∠ACB,90°-α=3(60°+α),α=-22.5°(舍);
综上,α=30°或52.5°,④正确。
正确结论个数为3,选C。
11. 为使一个四边形木架不变形,我们会沿其对角线钉一根木条,这是利用了三角形的
稳定性
.
答案:稳定性
12. 若三角形的两边长分别为2和5,第三边长为$a$,则$a$的取值范围是
$3 < a < 7$
.
答案:$3 < a < 7$
解析:
解:根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。
5 - 2 < a < 5 + 2
3 < a < 7
故答案为:3 < a < 7
13. 一个多边形的每个内角都相等,且每个内角的度数都是与它相邻外角度数的3倍,则这是
八
边形.
答案:八
解析:
设这个多边形的每个外角的度数为$x$,则每个内角的度数为$3x$。
因为多边形的一个内角与它相邻的外角互补,所以$x + 3x = 180^\circ$,
解得$4x = 180^\circ$,$x = 45^\circ$。
由于多边形的外角和为$360^\circ$,所以这个多边形的边数为$360^\circ ÷ 45^\circ = 8$。
八
14. 如图,在直角三角形$ABC$中,$∠ACB= 90^{\circ }$,$AC= 3$,$BC= 4$,$AB= 5$,则点$C到AB$的距离为
2.4
.
答案:2.4
解析:
解:设点$C$到$AB$的距离为$h$。
$\because \angle ACB = 90^{\circ}$,
$\therefore S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2} × 3 × 4 = 6$。
又$\because S_{\triangle ABC} = \frac{1}{2}AB \cdot h$,$AB = 5$,
$\therefore \frac{1}{2} × 5 × h = 6$,解得$h = \frac{12}{5} = 2.4$。
2.4
15. 如图,$∠A+∠B+∠C+∠D+∠E+∠F+∠G= n\cdot 90^{\circ }$,则$n= $
6
.
答案:6
解析:
连接BF,设BC与GF交于点O。
在△GOC中,∠G + ∠C + ∠GOC = 180°;在△BOF中,∠OBF + ∠OFB + ∠BOF = 180°。
因为∠GOC = ∠BOF,所以∠G + ∠C = ∠OBF + ∠OFB。
∠A + ∠B + ∠C + ∠D + ∠E + ∠F + ∠G = ∠A + ∠B + (∠OBF + ∠OFB) + ∠D + ∠E + ∠F = ∠A + (∠B + ∠OBF) + (∠OFB + ∠F) + ∠D + ∠E = ∠A + ∠ABF + ∠BFG + ∠D + ∠E。
五边形ABFED的内角和为(5 - 2)×180° = 540°,即∠A + ∠ABF + ∠BFG + ∠D + ∠E = 540°。
所以∠A + ∠B + ∠C + ∠D + ∠E + ∠F + ∠G = 540° = 6×90°,则n = 6。
6
16. 如图是一副三角板拼成的图案,则$∠AED$的度数为
105
$^{\circ }$.
答案:105
17. 如图,在$\triangle ABC$中,$∠A= 56^{\circ }$,点$D在AB$上,过点$D作DE// BC$,交$AC于点E$,$DP平分∠ADE$,交$∠ACB的平分线于点P$,$CP与DE相交于点G$,$∠ACF的平分线CQ与DP相交于点Q$,则$∠DQC= $
28
$^{\circ }$.
答案:1. 首先,因为$DE// BC$:
根据两直线平行,同位角相等,可得$\angle ADE=\angle B$,$\angle AED = \angle ACB$。
已知$\angle A = 56^{\circ}$,根据三角形内角和定理$\angle A+\angle B+\angle ACB = 180^{\circ}$,所以$\angle B+\angle ACB=180^{\circ}-\angle A = 124^{\circ}$。
又因为$\angle ACF=\angle A+\angle B$(三角形外角性质)。
2. 然后,根据角平分线的性质:
因为$DP$平分$\angle ADE$,设$\angle ADP=\angle PDE=\frac{1}{2}\angle ADE$;$CP$平分$\angle ACB$,设$\angle ACG=\angle BCG=\frac{1}{2}\angle ACB$;$CQ$平分$\angle ACF$,设$\angle ACQ=\angle FCQ=\frac{1}{2}\angle ACF$。
由$\angle ACF=\angle A+\angle B$,可得$\angle FCQ=\frac{1}{2}(\angle A+\angle B)$。
又因为$\angle DGC=\angle BCG+\angle B$(三角形外角性质,$\angle DGC$是$\triangle BCG$的外角),且$\angle PDE=\frac{1}{2}\angle B$。
根据三角形外角性质$\angle DQC=\angle FCQ - \angle PDE$。
把$\angle FCQ=\frac{1}{2}(\angle A+\angle B)$,$\angle PDE=\frac{1}{2}\angle B$代入$\angle DQC=\angle FCQ - \angle PDE$中。
则$\angle DQC=\frac{1}{2}(\angle A+\angle B)-\frac{1}{2}\angle B$。
3. 最后,化简求解:
对$\angle DQC=\frac{1}{2}(\angle A+\angle B)-\frac{1}{2}\angle B$进行化简,根据乘法分配律$a(b + c)=ab+ac$,这里$a=\frac{1}{2}$,$b = \angle A$,$c=\angle B$,$\angle DQC=\frac{1}{2}\angle A+\frac{1}{2}\angle B-\frac{1}{2}\angle B$。
所以$\angle DQC=\frac{1}{2}\angle A$。
已知$\angle A = 56^{\circ}$,则$\angle DQC = 28^{\circ}$。
故答案为:$28$。
解析:
解:
∵DE//BC,
∴∠ADE=∠B,∠AED=∠ACB。
∵DP平分∠ADE,
∴∠PDE=∠ADP=1/2∠ADE=1/2∠B。
∵CQ平分∠ACF,∠ACF=180°-∠ACB,
∴∠QCF=1/2∠ACF=90°-1/2∠ACB。
∵∠A=56°,
∴∠B+∠ACB=180°-∠A=124°。
在△DQC中,∠DQC=180°-∠QDC-∠QCD。
∠QDC=∠ADP=1/2∠B,∠QCD=∠QCF=90°-1/2∠ACB,
∴∠DQC=180°-1/2∠B-(90°-1/2∠ACB)=90°-1/2(∠B-∠ACB)。
又∠B+∠ACB=124°,
∴∠DQC=90°-1/2(124°-2∠ACB-∠ACB)(此步可简化为)
=90°-1/2(∠B+∠ACB)=90°-1/2×124°=90°-62°=28°。
28
18. (6分)一个三角形的三边长是三个连续的奇数,且三角形的周长小于30,求这个三角形三边的长.
答案:解:依题意设三角形的三边长分别为 $x - 2,x,x + 2$,$\therefore \left\{\begin{array}{l} x - 2 + x + x + 2 < 30,\\ x - 2 > 0,\end{array}\right.$ 解得 $2 < x < 10$,$\therefore x$ 最大取 9,最小取 3,且 $x$ 为奇数。当 $x = 9$ 时,三边的长分别为 7,9,11;当 $x = 7$ 时,三边的长分别为 5,7,9;当 $x = 5$ 时,三边的长分别为 3,5,7;当 $x = 3$ 时,三边的长分别为 1,3,5,此时不能构成三角形。综上,这个三角形三边的长分别为 7,9,11 或 5,7,9 或 3,5,7。
解析:
解:设三角形的三边长分别为 $x - 2$,$x$,$x + 2$($x$ 为奇数)。
根据题意,得:
$\begin{cases}(x - 2) + x + (x + 2) < 30 \\x - 2 > 0\end{cases}$
解得:$2 < x < 10$。
因为 $x$ 为奇数,所以 $x$ 可取 3,5,7,9。
当 $x = 3$ 时,三边长为 1,3,5,$1 + 3 = 4 < 5$,不能构成三角形;
当 $x = 5$ 时,三边长为 3,5,7,$3 + 5 > 7$,能构成三角形;
当 $x = 7$ 时,三边长为 5,7,9,$5 + 7 > 9$,能构成三角形;
当 $x = 9$ 时,三边长为 7,9,11,$7 + 9 > 11$,能构成三角形。
综上,这个三角形三边的长分别为 3,5,7 或 5,7,9 或 7,9,11。