8.若关于x的多项式$2x+a与-x^{2}+bx-2$的乘积展开式中没有二次项,且常数项为 20,求 a,b 的值.
答案:解:$(2x+a)(-x^{2}+bx-2)=-2x^{3}+(2b-a)x^{2}+(-4+ab)x-2a.$
∵展开式中没有二次项,且常数项为20,$\therefore 2b-a=0,-2a=20,$$\therefore a=-10,b=-5.$
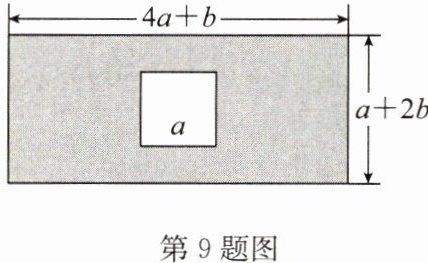
9.(2024 春·安庆期中)如图,现有一块长$(4a+b)$米,宽$(a+2b)$米的长方形地块,规划将阴影部分进行绿化,中间预留部分是边长为a米的正方形.
(1)求绿化的面积 S(用含 a,b 的代数式表示,并化简);
(2)若$a= 2,b= 3$,绿化成本为 100 元/平方米,则完成绿化共需要多少元?
答案:解:
(1)绿化的面积是$(4a+b)(a+2b)-a^{2}=(3a^{2}+9ab+2b^{2})$平方米.
(2)当$a=2,b=3$时,$100(3a^{2}+9ab+2b^{2})=100(3×2^{2}+9×2×3+2×3^{2})=8400$(元),即当$a=2,b=3$时,完成绿化共需要8400元.
10.甲、乙两人同时计算一道整式乘法题:$(2x+a)\cdot (3x+b)$.甲由于抄错了第一个多项式中a的符号,即把+a抄成了-a,得到的结果为$6x^{2}+11x-10$,乙由于抄漏了第二个多项式中 3x 的系数,即把 3x 抄成了 x,得到的结果为$2x^{2}-9x+10$,请你计算出这道整式乘法题的正确结果.
答案:解:$(2x-a)\cdot (3x+b)=6x^{2}+2bx-3ax-ab=6x^{2}+(2b-3a)x-ab,\therefore 2b-3a=11$ ①,$(2x+a)\cdot (x+b)=2x^{2}+2bx+ax+ab=2x^{2}+(2b+a)x+ab,\therefore 2b+a=-9$ ②,由①和②组成方程组$\left\{\begin{array}{l} 2b-3a=11,\\ 2b+a=-9,\end{array}\right. $解得$\left\{\begin{array}{l} a=-5,\\ b=-2,\end{array}\right. $$\therefore (2x-5)\cdot (3x-2)=6x^{2}-4x-15x+10=6x^{2}-19x+10.$
解析:
解:甲抄错 $a$ 的符号,计算 $(2x - a)(3x + b)$,展开得:
$\begin{aligned}(2x - a)(3x + b)&=6x^2 + 2bx - 3ax - ab\\&=6x^2 + (2b - 3a)x - ab\end{aligned}$
已知结果为 $6x^2 + 11x - 10$,故:
$2b - 3a = 11 \quad ①$
乙抄漏 $3x$ 的系数,计算 $(2x + a)(x + b)$,展开得:
$\begin{aligned}(2x + a)(x + b)&=2x^2 + 2bx + ax + ab\\&=2x^2 + (2b + a)x + ab\end{aligned}$
已知结果为 $2x^2 - 9x + 10$,故:
$2b + a = -9 \quad ②$
联立①②得方程组:
$\begin{cases}2b - 3a = 11 \\2b + a = -9\end{cases}$
解得:
$\begin{cases}a = -5 \\b = -2\end{cases}$
正确式子为 $(2x - 5)(3x - 2)$,展开得:
$\begin{aligned}(2x - 5)(3x - 2)&=6x^2 - 4x - 15x + 10\\&=6x^2 - 19x + 10\end{aligned}$
答:正确结果为 $6x^2 - 19x + 10$。