9. 为了解决某地区两个村庄的村民子女就近入学问题,某企业捐资助学,计划新建一所学校.如图,AB,AC 表示两条公路,点 M,N 表示两个村庄,学校的位置需满足三个条件:①到两条公路的距离相等;②到两个村庄的距离相等;③在$∠BAC$的内部.请运用尺规作图确定学校的位置,不写作法,保留作图痕迹并写明结论.
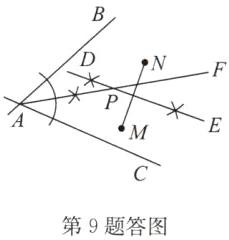
答案:解:点P为线段MN的垂直平分线与∠BAC的平分线的交点,则点P到点M,N的距离相等,到AB,AC的距离也相等,如答图.
10. 如图,已知$△ABC$为等腰直角三角形,$AC= BC= 4,∠BCD= 15^{\circ }$,P 为射线 CD 上的动点,求$|PA-PB|$的最大值.

答案:解:如答图,作点A关于CD的对称点A',连接A'B交CD于点P,则点P就是使|PA - PB|的值最大的点,|PA - PB|=A'B,连接A'C.
∵△ABC为等腰直角三角形,AC=BC=4,
∴∠CAB=∠ABC=45°,∠ACB=90°.
∵∠BCD=15°,
∴∠ACD=75°,
∴∠A'CD=75°,
∴∠ACA'=150°.
∵AC=A'C,
∴A'C=BC,∠CA'A=∠CAA'=15°.
∵∠ACB=90°,
∴∠A'CB=60°,
∴△A'BC是等边三角形,
∴A'B=BC=4.
故|PA - PB|的最大值为4.

11. 如图,在平面直角坐标系中,点 A 的坐标为$(1,0)$,以线段 OA 为边在第四象限内作等边三角形 AOB,C 为 x 轴正半轴上一动点$(OC>1)$,连接 BC,以线段 BC 为边在第四象限内作等边三角形 CBD,连接 DA 并延长,交 y 轴于点 E.
(1)$△OBC与△ABD$全等吗? 证明你的结论;
(2)当点 C 运动到什么位置时,以 A,E,C 为顶点的三角形是等腰三角形?

答案:解:
(1)△OBC≌△ABD.证明如下:
∵△AOB,△CBD都是等边三角形,
∴OB=AB,CB=DB,∠ABO=∠DBC,
∴∠OBC=∠ABD.
在△OBC和△ABD中,{OB = AB,∠OBC = ∠ABD,CB = DB,
∴△OBC≌△ABD(SAS).
(2)
∵△OBC≌△ABD,
∴∠BOC=∠BAD=60°.
又
∵∠OAB=60°,
∴∠OAE=180° - 60° - 60°=60°,
∴∠EAC=120°,∠OEA=30°,
∴当以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰.
∵在Rt△AOE中,OA=1,∠OEA=30°,
∴AE=2,
∴AC=AE=2,
∴OC=1 + 2=3,
∴当点C的坐标为(3,0)时,以A,E,C为顶点的三角形是等腰三角形.