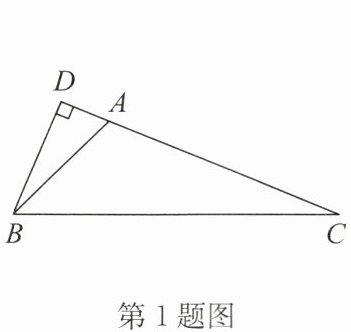
1. 如图,在$\triangle ABC$中,$\angle ABC = 45^{\circ}$,$\angle C = 22.5^{\circ}$,$BD \perp CA$,交$CA的延长线于点D$。若$AC = 8\mathrm{cm}$,则$BD = $
4
$\mathrm{cm}$。
答案:4
解析:
延长$CA$到点$E$,使$DE=AD$,连接$BE$。
因为$BD\perp CA$,所以$\angle ADB=\angle EDB=90^\circ$。
在$\triangle ADB$和$\triangle EDB$中,
$\begin{cases}AD=ED\\\angle ADB=\angle EDB\\BD=BD\end{cases}$,
所以$\triangle ADB\cong\triangle EDB(SAS)$,
所以$AB=EB$,$\angle E=\angle BAD$。
因为$\angle ABC=45^\circ$,$\angle C=22.5^\circ$,
所以$\angle BAC=180^\circ-\angle ABC-\angle C=112.5^\circ$,
所以$\angle BAD=180^\circ-\angle BAC=67.5^\circ$,
所以$\angle E=67.5^\circ$。
在$\triangle EBC$中,$\angle EBC=180^\circ-\angle E-\angle C=90^\circ$,
$\angle E=\angle EBC-\angle ABC=45^\circ$,
所以$\angle E=\angle EBC=45^\circ$,
所以$BC=EC$。
设$BD=x$,在$Rt\triangle BDC$中,$\angle C=22.5^\circ$,
则$DC=\frac{BD}{\tan\angle C}=\frac{x}{\tan22.5^\circ}$,
$AD=DE=DC-EC=DC-AC=DC-8$。
在$Rt\triangle ABD$中,$\tan\angle BAD=\frac{BD}{AD}$,
即$\tan67.5^\circ=\frac{x}{AD}$,$AD=\frac{x}{\tan67.5^\circ}$。
因为$\tan67.5^\circ=\tan(45^\circ+22.5^\circ)=\frac{1+\tan22.5^\circ}{1-\tan22.5^\circ}$,
设$t=\tan22.5^\circ$,则$\tan67.5^\circ=\frac{1+t}{1-t}$,
又因为$\tan45^\circ=\frac{2t}{1-t^2}=1$,解得$t=\sqrt{2}-1$(负值舍去),
所以$\tan67.5^\circ=\sqrt{2}+1$,$AD=\frac{x}{\sqrt{2}+1}=x(\sqrt{2}-1)$,
$DC=\frac{x}{\sqrt{2}-1}=x(\sqrt{2}+1)$。
因为$DC-AD=AC$,
所以$x(\sqrt{2}+1)-x(\sqrt{2}-1)=8$,
$2x=8$,$x=4$,即$BD=4$。
4
2. 如图,在四边形$ABCD$中,$AB = AD$,$\angle BAD = \angle BCD = 90^{\circ}$,连接$AC$。若$AC = \sqrt{6}$,则四边形$ABCD$的面积为______
3
。

答案:3
解析:
过点$A$作$AE \perp AC$,交$CD$的延长线于点$E$。
$\because \angle BAD = \angle BCD = 90^{\circ}$,
$\therefore \angle ADC + \angle ABC = 180^{\circ}$,$\angle EAD + \angle DAC = 90^{\circ}$,
又$\angle BAC + \angle DAC = 90^{\circ}$,$\therefore \angle EAD = \angle BAC$。
$\because \angle ADE + \angle ADC = 180^{\circ}$,$\therefore \angle ADE = \angle ABC$。
又$AD = AB$,$\therefore \triangle ADE \cong \triangle ABC$(AAS)。
$\therefore AE = AC = \sqrt{6}$,$S_{\triangle ADE} = S_{\triangle ABC}$。
$\therefore$四边形$ABCD$的面积$= S_{\triangle ADC} + S_{\triangle ABC} = S_{\triangle ADC} + S_{\triangle ADE} = S_{\triangle ACE}$。
$\because \triangle ACE$是等腰直角三角形,
$\therefore S_{\triangle ACE} = \frac{1}{2} × AC × AE = \frac{1}{2} × \sqrt{6} × \sqrt{6} = 3$。
3
3. 如图,在$\triangle ABC$中,$AB = BC$,$AB \perp BC$,$B(0,2)$,$C(2,-2)$,求点$A$的坐标。

答案:解:如答图,作CM⊥y轴于点M.
∵B(0,2),C(2,−2),
∴CM=BO=OM=2,
∴BM=4.在Rt△AOB和Rt△BMC中,{AB=BC, BO=CM,
∴Rt△AOB≌Rt△BMC(HL),
∴AO=BM=4,
∴点A的坐标为(−4,0).
4. 如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC = 90^{\circ}$,$D为BC$上一点,过点$D作DE \perp AD$,且$DE = AD$,连接$BE$,求$\angle DBE$的度数。

答案:解:如答图,作AM⊥BC于点M,作EN⊥BC于点N,
∴∠END=90°.
∵AB=AC,∠BAC=90°,AM⊥BC,
∴AM=MB=CM,∠AMD=90°.
∵AD⊥DE,
∴∠ADE=90°,
∴∠ADM+∠EDN=90°,∠EDN+∠NED=90°,
∴∠MDA=∠NED.
∵AD=DE,
∴△AMD≌△DNE(AAS),
∴DM=EN,DN=AM=BM,
∴DN−MN=BM−NM,即DM=BN,
∴BN=EN,
∴∠DBE=45°.
5. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,$D是AC$边上一点,连接$BD$,$EC \perp AC$,垂足为$C$,且$AE = BD$,$AE交线段BC于点F$。
(1)在图中画出符合题意的图形,并证明$CE = AD$;
(2)当$\angle CFE = \angle ADB$时,求证:$BD平分\angle ABC$。

答案:
(1)解:画出图形如答图.证明:在Rt△ACE和Rt△BAD中,{AE=BD, AC=BA,
∴Rt△ACE≌Rt△BAD(HL),
∴CE=AD;
(2)证明:
∵Rt△ACE≌Rt△BAD,
∴∠E=∠ADB.
∵∠CFE=∠ADB,
∴∠CFE=∠E.
∵∠ACE+∠DAB=180°,
∴CE//AB,
∴∠E=∠FAB.
∵∠CFE=∠AFB,
∴∠BAF=∠AFB.
∵∠ADB=∠E=∠EAB,
∴AE⊥BD,
∴∠EAB+∠ABD=90°,∠AFB+∠FBD=90°,
∴∠ABD=∠FBD,
∴BD平分∠ABC.