6. 请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹。
(1) 如图①,在四边形$ABCD$中,$AB = AD$,$\angle B = \angle D$,$BC = CD$,画出四边形$ABCD的对称轴m$;
(2) 如图②,在四边形$ABCD$中,$AD// BC$,$\angle A = \angle D$,画出$BC边的垂直平分线n$。
答案:解:
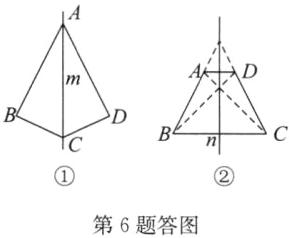
(1)如答图①,直线m即为所求.
(2)如答图②,直线n即为所求.
7. 如图,在$\triangle ABC$中,$AD是\angle BAC$的平分线,$AD的垂直平分线交AB于点E$,交$CB的延长线于点F$,连接$DE$,$AF$。
(1) 判断$DE与AC$的位置关系,并证明你的结论;
(2) 求证:$\angle C = \angle EAF$。


答案:
(1)解:DE//AC.理由如下:
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD.
∵EF垂直平分AD,
∴AE=DE,
∴∠BAD=∠EDA,
∴∠CAD=∠EDA,
∴DE//AC;
(2)证明:
∵EF垂直平分AD,
∴EA=ED,FA=FD.在△AEF和△DEF中,{EA=ED,EF=EF,FA=FD,
∴△AEF≌△DEF(SSS),
∴∠EAF=∠EDF.
∵DE//AC,
∴∠C=∠EDF,
∴∠C=∠EAF.
8. 请按要求完成下面问题。
(1) 如图①,$AB = AC$,这两条线段一定关于$\angle BAC$的______所在的直线对称,请画出该直线;
(2) 如图②,已知线段$AB和点C$,求作线段$CD$,使它与线段$AB$成轴对称,且点$A与点C$是对称点,对称轴是线段$AC$的______;
(3) 如图③,任意位置(不成轴对称)的两条线段$AB$,$CD$,$AB = CD$。你能利用从(1)(2)中获得的启示,对其中一条线段作两次轴对称使它们重合吗?如果能,请画出图形并简要描述作图步骤;如果不能,请说明理由。

答案:(1)平分线 如答图①,作∠BAC的平分线所在的直线a,则a即为所求.(画对称轴方法不唯一)

(2)垂直平分线 如答图②,线段CD即为所求.

(3)解:能.如答图③所示,连接BD;作线段BD的垂直平分线c,即为对称轴;作点C关于直线c的对称点E;连接BE;作∠ABE的平分线所在直线d,即为对称轴.故线段CD经过两次轴对称可与线段AB重合.(方法不唯一)
