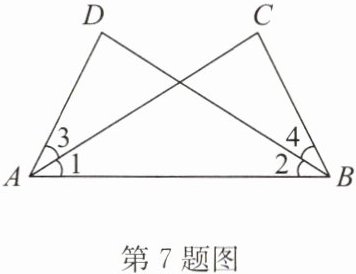
7. 如图,在$\triangle ABC和\triangle BAD$中,$\angle 1 = \angle 2$,$\angle 3 = \angle 4$. 求证:$AC = BD$.
答案:证明:
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠DAB=∠CBA.
在△ADB和△BCA中,$\left\{\begin{array}{l} ∠2=∠1,\\ AB=BA,\\ ∠DAB=∠CBA,\end{array}\right. $
∴△ADB≌△BCA(ASA),
∴AC=BD.
8. 如图,$AC\perp CF于点C$,$DF\perp CF于点F$,$AB与DE交于点O$,且$EC = BF$,$AB = DE$,求证:$AE = DB$.

答案:证明:
∵AC⊥CF,DF⊥CF,
∴∠ACB=∠DFE=90°.
∵EC=BF,
∴EC+EB=BF+EB,即CB=FE.
在Rt△ACB与Rt△DFE中,$\left\{\begin{array}{l} AB=DE,\\ CB=FE,\end{array}\right. $
∴Rt△ACB≌Rt△DFE(HL),
∴AC=DF.
在△ACE与△DFB中,$\left\{\begin{array}{l} AC=DF,\\ ∠ACE=∠DFB,\\ CE=FB,\end{array}\right. $
∴△ACE≌△DFB(SAS),
∴AE=DB.
9. 如图,在$\triangle ABC$中,$D是边BC$的中点,连接$AD并延长到点E$,使$DE = AD$,连接$CE$.
(1)求证:$\triangle ABD\cong \triangle ECD$;
(2)若$\triangle ABD的面积为5$,求$\triangle ACE$的面积.

答案:
(1)证明:
∵D是BC的中点,
∴BD=CD.
在△ABD与△ECD中,$\left\{\begin{array}{l} BD=CD,\\ ∠ADB=∠EDC,\\ AD=ED,\end{array}\right. $
∴△ABD≌△ECD(SAS).
(2)解:在△ABC中,D是边BC的中点,
$∴S_{△ABD}=S_{△ADC},$
∵△ABD≌△ECD,
$∴S_{△ABD}=S_{△ECD}.$
$∵S_{△ABD}=5,$
$∴S_{△ACE}=S_{△ACD}+S_{△ECD}=5+5=10,$
∴△ACE的面积为10.
10. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CE\perp AB于点E$,$AD = AC$,$AF平分\angle CAB交CE于点F$,连接$DF$并延长,交$AC于点G$.
(1)若$\angle B = 40^{\circ}$,求$\angle ADF$的度数;
(2)求证:$FG = FE$.

答案:
(1)解:
∵AF平分∠CAB,
∴∠CAF=∠DAF.
在△ACF和△ADF中,$\left\{\begin{array}{l} AC=AD,\\ ∠CAF=∠DAF,\\ AF=AF,\end{array}\right. $
∴△ACF≌△ADF(SAS),
∴∠ACF=∠ADF.
∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠CAE=90°,∠CAE+∠B=90°,
∴∠ACF=∠B,
∴∠ADF=∠B=40°.
(2)证明:由
(1)知∠ADF=∠B,
∴DF//BC.
∵BC⊥AC,
∴FG⊥AC.
又FE⊥AB,AF平分∠CAB,
∴FG=FE.