1. (2024 秋·滨海新区期末)把 $5(a - b)+m(b - a)$ 提公因式后一个因式是 $a - b$,则另一个因式是(
A
)
A.$5 - m$
B.$5 + m$
C.$m - 5$
D.$-m - 5$
答案:A
解析:
$5(a - b)+m(b - a)$
$=5(a - b)-m(a - b)$
$=(a - b)(5 - m)$
另一个因式是$5 - m$
A
2. 把多项式 $x^{2}y^{5}-xy^{n}z$ 因式分解时,提取的公因式是 $xy^{5}$,则 $n$ 的值可能为(
A
)
A.6
B.4
C.3
D.2
答案:A
解析:
要对多项式$x^{2}y^{5}-xy^{n}z$提取公因式$xy^{5}$,需满足:
对于字母$x$,各项最低次幂为$1$,符合公因式中$x$的次数。
对于字母$y$,各项最低次幂应为$5$,所以$n\geq5$。
选项中只有$6\geq5$,故$n$的值可能为$6$。
A
3. (2024 秋·西城区期末)已知等式:$x(y - 1)+$
3y-3
$=(y - 1)(x + 3)$,若横线上所填的式子记为 $A$,则 $A= $
3y-3
.
答案:3y-3
解析:
$A=(y - 1)(x + 3)-x(y - 1)$
$=(y - 1)[(x + 3)-x]$
$=(y - 1)×3$
$=3y - 3$
$3y - 3$
4. 若实数 $a$,$b$ 满足 $a + b = 5$,$a^{2}b + ab^{2}= -15$,则 $ab$ 的值是
-3
.
答案:-3
解析:
解:因为$a + b = 5$,$a^{2}b + ab^{2}=-15$,
而$a^{2}b + ab^{2}=ab(a + b)$,
所以$ab(a + b)=-15$,
将$a + b = 5$代入上式,得$5ab=-15$,
解得$ab=-3$。
-3
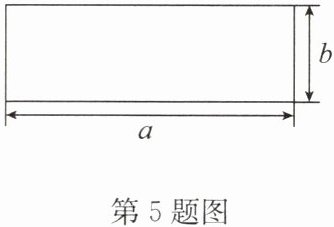
5. (2024·福田区二模)如图,长方形的长、宽分别为 $a$,$b$,且 $a$ 比 $b$ 大 3,面积为 7,则 $a^{2}b - ab^{2}$ 的值为______
21
.
答案:21
解析:
由题意得,$a - b = 3$,$ab = 7$。
$a^{2}b - ab^{2} = ab(a - b)$
将$a - b = 3$,$ab = 7$代入上式,得:
$7×3 = 21$
21
6. 对下列多项式进行因式分解:
(1)$2x^{2}y^{3}-4x^{3}y^{2}-6xy$; (2)$-6a^{3}-10a^{2}-2a$;
(3)$3m(x + y)-9n(x + y)$; (4)$(x - 3)^{2}+3x - 9$.
答案:解:
(1)原式=2xy(xy²-2x²y-3).
(2)原式=-2a(3a²+5a+1).
(3)原式=3(x+y)(m-3n).
(4)原式=x(x-3).
7. (2024 春·西安期末)如图是甲、乙两位同学因式分解 $-x^{2}+x$ 的结果,下列判断正确的是(
A
)
A.甲、乙的结果都正确
B.甲、乙的结果都不正确
C.只有甲的结果正确
D.只有乙的结果正确
答案:A
解析:
甲同学:$-x^{2}+x=-x(x-1)$,正确;
乙同学:$-x^{2}+x=x(1-x)$,正确;
A
8. 已知 $M = a^{2}-2a$,$a= \sqrt{7}+1$,则 $M$ 的值为
6
.
答案:6
解析:
$M=a^{2}-2a$,将$a = \sqrt{7}+1$代入得:
$\begin{aligned}M&=(\sqrt{7}+1)^{2}-2(\sqrt{7}+1)\\&=7 + 2\sqrt{7}+1 - 2\sqrt{7}-2\\&=(7 + 1 - 2)+(2\sqrt{7}-2\sqrt{7})\\&=6 + 0\\&=6\end{aligned}$
6
9. 已知 $(2x - 21)(3x - 7)-(3x - 7)(x - 13)$ 可分解因式为 $(3x + a)(x + b)$,其中 $a$,$b$ 均为整数,则 $a + 3b$ 的值为
-31
.
答案:-31
解析:
$(2x - 21)(3x - 7)-(3x - 7)(x - 13)$
$=(3x - 7)[(2x - 21)-(x - 13)]$
$=(3x - 7)(2x - 21 - x + 13)$
$=(3x - 7)(x - 8)$
因为分解因式为$(3x + a)(x + b)$,所以$a=-7$,$b=-8$。
$a + 3b=-7 + 3×(-8)=-7 - 24=-31$
$-31$