7. 计算:
(1)$(a+2b-3c)^{2};$
(2)$(2x-3y+z)(2x+3y-z);$
(3)$(m+n+2)(m+n-2)-m(m+4n).$
答案:
(1)原式$=a^{2}+4b^{2}+9c^{2}+4ab-6ac-12bc.$
(2)原式$=[2x-(3y-z)][2x+(3y-z)]=4x^{2}-(3y-z)^{2}=4x^{2}-(9y^{2}-6yz+z^{2})=4x^{2}-9y^{2}+6yz-z^{2}.$
(3)原式$=m^{2}+2mn+n^{2}-4-m^{2}-4mn=n^{2}-2mn-4.$
8. (1)已知:$x^{2}+2y^{2}-2xy+4y+4= 0$,求$x^{2}+y^{2}$的值;
(2)已知等腰三角形 ABC 的三边长分别为a,b,c,其中a,b满足$a^{2}+b^{2}+45= 12a+6b$,求$\triangle ABC$的周长.
答案:
(1)$x^{2}+2y^{2}-2xy+4y+4=0,$
$(x^{2}-2xy+y^{2})+(y^{2}+4y+4)=0,$
$(x-y)^{2}+(y+2)^{2}=0.$
$\because (x-y)^{2}≥0,(y+2)^{2}≥0,\therefore x-y=0,y+2=0,$
$\therefore x=y=-2,\therefore x^{2}+y^{2}=8.$
(2)$a^{2}+b^{2}+45=12a+6b,$
$(a^{2}-12a+36)+(b^{2}-6b+9)=0,$
$(a-6)^{2}+(b-3)^{2}=0.$
$\because (a-6)^{2}≥0,(b-3)^{2}≥0,\therefore a-6=0,b-3=0,$
$\therefore a=6,b=3.\because △ABC$为等腰三角形,
$\therefore c=6,\therefore △ABC$的周长是 15.
9. 阅读材料:若$a+b= 3,ab= 1$,求$a^{2}+b^{2}$的值.
解:因为$a+b= 3$,所以$(a+b)^{2}= 9$,即:$a^{2}+2ab+b^{2}= 9,$
又因为$ab= 1$,所以$a^{2}+b^{2}= 7.$
根据上面的解题思路与方法,解决下列问题:
(1)若$x+y= 8,x^{2}+y^{2}= 40$,求xy的值;
解:$\because x+y=8,\therefore (x+y)^{2}=x^{2}+2xy+y^{2}=64,$
又$x^{2}+y^{2}=40,\therefore 2xy=24,xy=12.$
(2)若$(4-x)x= 5$,则$(4-x)^{2}+x^{2}=$
6
;
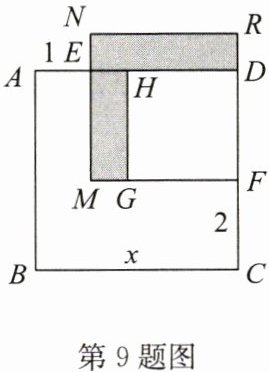
(3)如图,已知正方形 ABCD 的边长为x,E,F 分别是 AD,DC 上的点,且$AE= 1,CF= 2$,长方形 EMFD 的面积是 12,分别以 MF,DF 为边作正方形 MFRN 和正方形 GFDFH,则x的值为
5
.
答案:
(1)解:$\because x+y=8,\therefore (x+y)^{2}=x^{2}+2xy+y^{2}=64,$
又$x^{2}+y^{2}=40,\therefore 2xy=24,xy=12.$
(2)6
(3)5