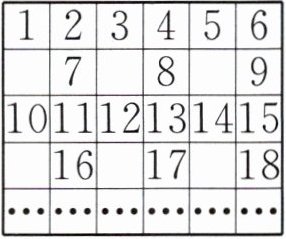
答案：[跟踪练习1] $ 31÷2=15 $（组）$\cdots\cdots1$（行） 第31行第3列是 $ 15×9+3=138 $。 $ 2025÷9=225 $（组） $ 225×2=450 $（行） 2025在第450行第6列。

答案：解析：本题主要考查周期规律问题的应用。
由题可知，每$8+2=10$（颗）珠子为一个周期，所以30颗珠子中有3个周期，每个周期的最后两颗珠子为黑色。
蜜蜂从第2颗黑色珠子起飞，即从第10颗珠子起飞，沿顺时针方向，每次飞过6颗珠子落到下一颗珠子上，即每次飞过$6+1=7$（颗）珠子。
设蜜蜂飞了n次后落到黑色珠子上，则它落到的珠子位置可以表示为$10+7n$。
需要找到一个最小的正整数n，使得$10+7n$是10的倍数加9或10（即黑色珠子的位置）。
通过试验或计算，可以发现当$n=7$时，$10+7n=59$，59除以10的余数为9，即蜜蜂落到了第29颗珠子上，是黑色珠子。
答案：至少飞7次才能再次落到黑色珠子上。

答案：[跟踪练习2] 这只飞虫至少要飞5次才能再次落到红色珠子上。 解析·根据题意可知，每$ 1+4=5 $（颗）珠子为一个周期，因此可以推出20颗珠子中第1颗、第6颗、第11颗和第16颗都是红色珠子。这只飞虫从第1颗红色珠子起飞，沿顺时针方向，每次飞过5颗珠子落到下一颗珠子上休息，也就是 $ 5+1=6 $（颗）珠子为一个周期，所以第1次落到第7颗珠子上，第2次落到第13颗珠子上……即第1颗 $\xrightarrow[\text{第1次}]{}$ 第7颗 $\xrightarrow[\text{第2次}]{}$ 第13颗 $\xrightarrow[\text{第3次}]{}$ 第19颗 $\xrightarrow[\text{第4次}]{}$ 第25颗（第5颗） $\xrightarrow[\text{第5次}]{}$ 第31颗（第11颗）。因此这只飞虫至少要飞5次才能再次落到红色珠子上。