例1 (教材P83)经过纸上2个点可以画1条直线,经过3个点中的每两个点最多可以画3条直线,经过4个点中的每两个点最多可以画几条直线?经过5个、6个……点呢?画一画,数一数,你能找到其中的规律吗?
规范解答:
经过4个点中的每两个点最多可以画6条直线;
经过5个点中的每两个点最多可以画10条直线;
经过6个点中的每两个点最多可以画15条直线;
规律:当有n个点时,经过n个点中的每两个点最多可以画$[n×(n - 1)÷2]$条直线。
答案:规范解答:
经过4个点中的每两个点最多可以画6条直线;
经过5个点中的每两个点最多可以画10条直线;
经过6个点中的每两个点最多可以画15条直线;
规律:当有n个点时,经过n个点中的每两个点最多可以画$[n×(n - 1)÷2]$条直线。
过1个点可以画(
无数
)条直线,过9个点中的任意两个点最多可以画(
36
)条直线,过(
12
)个点中的任意两个点最多可以画66条直线。
答案:无数 36 12
解析:
过1个点可以画无数条直线。
过9个点中的任意两个点最多可以画的直线条数:从9个点中选2个点的组合数,即$C_{9}^2=\frac{9×8}{2×1}=36$条。
设过$n$个点中的任意两个点最多可以画66条直线,可得组合数公式$C_{n}^2=\frac{n(n - 1)}{2}=66$,解方程$n(n - 1)=132$,$n^2 - n - 132=0$,$(n - 12)(n + 11)=0$,解得$n=12$($n=-11$舍去)。
无数;36;12
例2 (教材P88)下边每个图中的∠1和∠2相等吗?为什么?
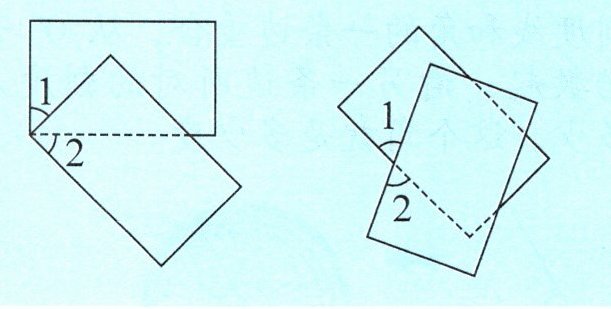
答案:相等。
第一个图:∠1和∠2与公共角∠3分别组成直角,∠1=90°-∠3,∠2=90°-∠3,所以∠1=∠2。
第二个图:∠1和∠2与公共角∠3分别组成平角,∠1=180°-∠3,∠2=180°-∠3,所以∠1=∠2。