用若干个小正方体摆一个物体,使得从前面看到的是,
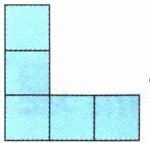
从上面看到的是。

摆这个物体,最少需要(
6
)个小正方体,最多需要(
8
)个小正方体。(只考虑面与面接触)
答案:6 8
解析:
解:从上面看,物体底层小正方体的排列为:前排2个,后排3个(左右各1个,中间1个),共5个。
从前面看,物体有两层。底层与从上面看的底层对应,共5个;上层最少在后排中间和前排中间各放1个,共2个,最少总个数:5+1=6(个);上层最多在后排中间、前排左右各放1个,共3个,最多总个数:5+3=8(个)。
最少需要6个,最多需要8个。
6 8
一个立体图形,从上面看到的形状是,

从左面看到的形状是,

搭这样的立体图形最少需要(
5
)个小正方体,最多需要(
8
)个小正方体。
答案:5 8
解析:
解:从上面看,底层小正方体排列为前排3个,后排左边1个,共4个。
从左面看,立体图形有两层。
最少情况:上层在后排左边1个小正方体上放1个,共4+1=5个。
最多情况:上层在底层前排3个和后排左边1个小正方体上各放1个,共4+4=8个。
答案:5;8
例 下面的物体是由8个同样大的正方体拼成的,先把这个物体的表面全部涂上蓝色,再拆开,会看到:

只有1个面涂蓝色的正方体有(
1
)个,只有2个面涂蓝色的正方体有(
0
)个,只有3个面涂蓝色的正方体有(
1
)个,只有4个面涂蓝色的正方体有(
4
)个,只有5个面涂蓝色的正方体有(
2
)个。
答案:只有1个面涂蓝色的正方体有(1)个,只有2个面涂蓝色的正方体有(0)个,只有3个面涂蓝色的正方体有(1)个,只有4个面涂蓝色的正方体有(4)个,只有5个面涂蓝色的正方体有(2)个。
下图是由3层小正方体组成的物体,把它的表面(包括底面,底面是正方形)都涂上色,再把小正方体分开,有(
16
)个小正方体是3面涂色的。
答案:16 解析·从下往上数,第一层中 3 面涂色的是每边中间的 3 个小正方体,共有 $ 3 × 4 = 12 $(个);第二层中 3 面涂色的是四个角上的小正方体,共有 4 个;第三层没有 3 面涂色的小正方体。所以 3 面涂色的小正方体共有 $ 12 + 4 = 16 $(个)。
解析:
解:第一层3面涂色的小正方体:每边中间有3个,共$3×4=12$(个);
第二层3面涂色的小正方体:四个角上各1个,共4个;
第三层没有3面涂色的小正方体。
$12+4=16$(个)
答:有16个小正方体是3面涂色的。