1. 下面是四年级四个班男生、女生的植树情况。
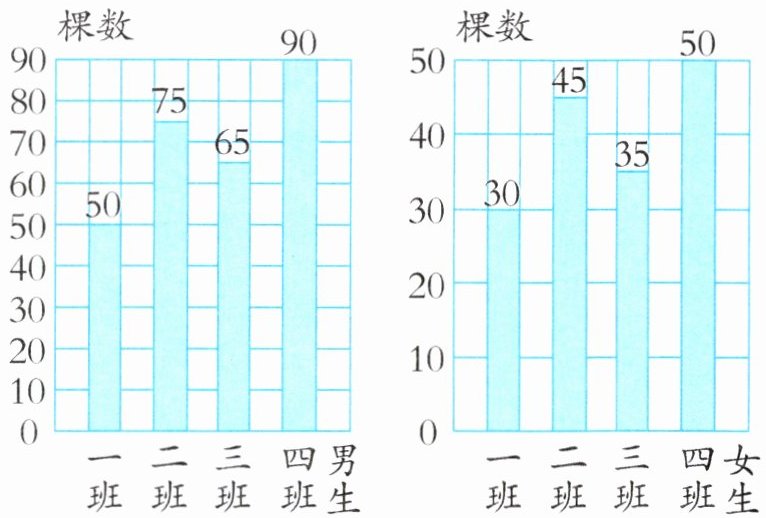
(1)四年级女生平均每班植树( )棵。请在图中画一画,移一移。
(2)四年级男生平均每班植树棵数比女生多( )棵。
答案:1. (1) 40
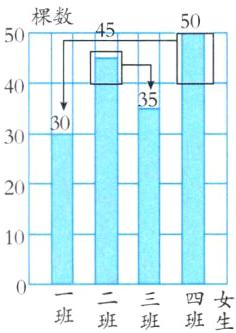
(2) 30
2. (1)在一次体育测试中,四年级平均每班的达标人数为35(各班达标人数不全相同)。下面说法正确的有(
B
)个。
① 二班达标人数最少,是36。
② 一班达标人数可能是35。
③ 三班达标人数最多,可能是35。
④ 六班达标人数可能是45。
A.1
B.2
C.3
D.4
答案:2. (1) B
解析:
解:①二班达标人数最少,若为36,则各班达标人数均≥36,平均每班达标人数≥36,与平均35矛盾,错误;
②一班达标人数可能是35,因各班达标人数不全相同,部分班级可为35,正确;
③三班达标人数最多,若为35,则各班达标人数均≤35,平均每班达标人数≤35,又因各班不全相同,平均<35,与平均35矛盾,错误;
④六班达标人数可能是45,其他班级达标人数可小于35,使总平均为35,正确。
正确的有②④,共2个。
答案:B
(2)学校足球队员的平均体重是45千克。王华的体重是38千克,王华加入足球队后,足球队员的平均体重(
B
)。
A.高于45千克
B.低于45千克
C.等于45千克
D.无法确定
答案:2. (2) B
解析:
解:设原来足球队有n名队员,总体重为45n千克。王华加入后,队员人数为n+1名,总体重为45n + 38千克,新平均体重为(45n + 38)/(n + 1)。因为38 < 45,所以(45n + 38)/(n + 1) < 45,即平均体重低于45千克。
B
3. (连云港灌云县期末)图中直条分别表示小明、小红和小华的身高,虚线中(
③
)的高度最接近他们的平均身高。

答案:3. ③
4. 新素养 应用意识 某小学举行演讲比赛,由五位评委打分,计分时,先去掉一个最高分和一个最低分,再算出其余三个分数的平均分作为选手的最后得分。下表是一位选手的记分单(单位:分),评委5打了(
85
)分。
|评委1|评委2|评委3|评委4|评委5|最后得分|
|79|83|86|81| |83|
答案:4. 85
解析:
设评委5打了$x$分。
已知最后得分是83分,由题意得,去掉一个最高分和一个最低分后,剩余三个分数的总和为$83×3 = 249$分。
列出已知分数:79、83、86、81、$x$。
假设$x$不是最高分也不是最低分,则剩余分数为83、81、$x$或79、83、$x$等,经计算:
若剩余分数为83、81、$x$,则$83 + 81 + x=249$,解得$x = 85$。
此时五个分数为79、81、83、85、86,去掉最高分86和最低分79,剩余81、83、85,其平均分为$(81 + 83 + 85)÷3=249÷3 = 83$,符合题意。
评委5打了85分。
答案:85
5. (2025·泰州兴化市期中)在音乐节中,甲、乙、丙三人的表现很出色。甲、乙两人的平均成绩是91分,乙、丙两人的平均成绩是92分,甲、丙两人的平均成绩是93分,三人的平均成绩是(
92
)分。
答案:5. 92 解析 甲+乙=91×2=182(分),乙+丙=92×2=184(分),甲+丙=93×2=186(分),甲+乙+丙=(182+184+186)÷2=276(分),平均成绩:276÷3=92(分)。
解析:
解:甲+乙=91×2=182(分)
乙+丙=92×2=184(分)
甲+丙=93×2=186(分)
甲+乙+丙=(182+184+186)÷2=276(分)
三人平均成绩=276÷3=92(分)
答:三人的平均成绩是92分。
6. 有5个数,平均数是10,如果把其中的一个数改为2,那么这5个数的平均数是9,这个被改动的数原来是(
7
)。
答案:6. 7 解析 先求出改动前5个数的总和是5×10=50,再求出改动后5个数的总和是5×9=45,总和少了50 - 45=5,可知把原数改小了5,因此原数是5+2=7。
解析:
解:改动前5个数的总和:5×10=50
改动后5个数的总和:5×9=45
总和减少的值:50-45=5
被改动的原数:2+5=7
答案:7