10.「2025 黑龙江齐齐哈尔建华期末,★☆」在围棋盒中有 x 枚白色棋子和 y 枚黑色棋子,从盒中随机取出一枚棋子,取得白色棋子的概率是$\frac{2}{5}$,如果再往盒中放进 3 枚黑色棋子,从盒中随机取出一枚棋子,取得白色棋子的概率为$\frac{1}{4}$,则原来盒里有白色棋子(
A
)
A.2 枚
B.3 枚
C.4 枚
D.5 枚
答案:10.A 由题意得$\begin{cases}\frac{x}{x + y}=\frac{2}{5},\\\frac{x}{x + y + 3}=\frac{1}{4},\end{cases}$ 解得$\begin{cases}x = 2,\\y = 3,\end{cases}$ ∴原来盒里有白色棋子2枚.故选A.
11.「2023 山东烟台中考,★☆」如图,在正方形中,阴影部分是以正方形的顶点及其对称中心为圆心,以正方形边长的一半为半径作弧形成的封闭图形.将一个小球在该正方形内自由滚动,小球随机停在正方形内的某一点上.若小球停在阴影部分的概率为$P_{1}$,停在空白部分的概率为$P_{2}$,则$P_{1}与P_{2}$的大小关系为( )
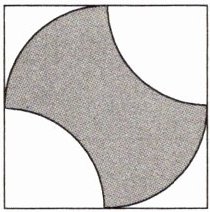
A.$P_{1}\lt P_{2}$
B.$P_{1}= P_{2}$
C.$P_{1}\gt P_{2}$
D.无法判断
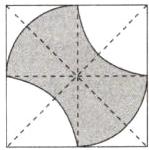
答案:11.B 如图,设正方形的边长为2a,则空白部分的面积为$2\times\frac{1}{4}\times\pi\cdot a^{2}+2\left(a^{2}-\frac{1}{4}\times\pi\cdot a^{2}\right)=\frac{1}{2}\pi a^{2}+2a^{2}-\frac{1}{2}\pi a^{2}=2a^{2}$,阴影部分的面积为$(2a)^{2}-2a^{2}=4a^{2}-2a^{2}=2a^{2}$,所以$P_{1}=\frac{\text{阴影部分面积}}{\text{正方形的面积}}=\frac{2a^{2}}{4a^{2}}=\frac{1}{2}$,$P_{2}=\frac{\text{空白部分面积}}{\text{正方形的面积}}=\frac{2a^{2}}{4a^{2}}=\frac{1}{2}$,所以$P_{1}=P_{2}$,故选B.
12.「2022 辽宁盘锦中考,★☆」若关于 x 的方程$x^{2}-3x + m = 0$有两个不相等的实数根,且$m\geq - 3$,则从满足条件的所有整数 m 中随机选取一个,恰好是负数的概率是______
$\frac{1}{2}$
.
答案:12.答案$\frac{1}{2}$
解析 ∵关于x的方程$x^{2}-3x + m = 0$有两个不相等的实数根,∴$\Delta = (-3)^{2}-4\times1\times m>0$,解得$m<\frac{9}{4}$,又∵$m\geq - 3$,∴$-3\leq m<\frac{9}{4}$,∴满足条件的所有整数为$-3$、$-2$、$-1$、$0$、$1$、$2$,共6个,其中负数有$-3$、$-2$、$-1$,共3个,∴从满足条件的所有整数m中随机选取一个,恰好是负数的概率是$\frac{3}{6}=\frac{1}{2}$.
13.「2024 山东菏泽成武开学测试,★☆」在不透明的口袋里放入除颜色外其余都相同的 6 个红球和一些黑球,从口袋里任意摸出一个球,如果摸到黑球的概率是$\frac{3}{5}$,那么口袋里放了
9
个黑球.要使摸到黑球的概率变成$\frac{3}{4}$,可以从口袋里拿走
3
个红球,也可以往口袋里再放入
9
个黑球.
答案:13.答案9;3;9
解析 设口袋里放了x个黑球,∵摸到黑球的概率是$\frac{3}{5}$,∴$\frac{x}{x + 6}=\frac{3}{5}$,解得$x = 9$,经检验,$x = 9$是原分式方程的解,且符合题意,∴口袋里放了9个黑球.设可以拿走y个红球,∵摸到黑球的概率变成$\frac{3}{4}$,∴$\frac{9}{15 - y}=\frac{3}{4}$,解得$y = 3$,经检验,$y = 3$是原分式方程的解,且符合题意,∴可以拿走3个红球.设可以往口袋里再放入z个黑球,∵摸到黑球的概率变成$\frac{3}{4}$,∴$\frac{9 + z}{15 + z}=\frac{3}{4}$,解得$z = 9$,经检验,$z = 9$是原分式方程的解,且符合题意,∴可以往口袋里再放入9个黑球.
14.「2025 四川成都温江期中,★☆」现有 6 张正面分别标有数字 0,1,2,3,4,5 的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为 a,则使得关于 x 的一元二次方程$x^{2}-2x+\frac{a}{2}= 0$有实数根,且关于 x 的分式方程$\frac{1 - ax}{x - 2}+2= \frac{1}{2 - x}$有解的概率为
$\frac{1}{6}$
.
答案:14.答案$\frac{1}{6}$
解析 ∵关于x的一元二次方程$x^{2}-2x+\frac{a}{2}=0$有实数根,∴$\Delta = (-2)^{2}-4\times1\times\frac{a}{2}=4 - 2a\geq0$,解得$a\leq2$.由分式方程$\frac{1 - ax}{x - 2}+2=\frac{1}{2 - x}$,得$\frac{ax - 1 + 2(2 - x)}{2 - x}=\frac{1}{2 - x}$,解得$x=\frac{2}{2 - a}(x\neq2)$,∴$a\neq1$且$a\neq2$,∴$a<2$且$a\neq1$.由题意得,共有6种等可能的结果,其中满足$a<2$且$a\neq1$的结果是$a = 0$,共1种,∴使得关于x的一元二次方程$x^{2}-2x+\frac{a}{2}=0$有实数根,且关于x的分式方程$\frac{1 - ax}{x - 2}+2=\frac{1}{2 - x}$有解的概率为$\frac{1}{6}$.
15.新课标几何直观斐波那契螺旋线也称“黄金螺旋线”,是根据斐波那契数列 1,1,2,3,5,…画出来的螺旋曲线.如图,白色小圆内切于边长为 1 的正方形,黑色曲线就是斐波那契螺旋线的一部分,它是依次在以 1,2,3,5 为边长的正方形中画一个圆心角为$90^{\circ}$的扇形,将其圆弧连接起来得到的.若在矩形 ABCD 内随机取一点,则此点取自阴影部分的概率是(
D
)

A.$\frac{\pi}{4}$
B.$\frac{39\pi}{160}$
C.$\frac{19\pi + 1}{80}$
D.$\frac{19\pi + 2}{80}$
答案:15.D 由题意得矩形ABCD的长为8,宽为5,即$S_{\text{矩形}ABCD}=8\times5 = 40$,因为$S_{\text{阴影}}=\left(1-\frac{\pi}{4}\right)+\frac{\pi}{4}+\frac{4\pi}{4}+\frac{9\pi}{4}+\frac{25\pi}{4}=\frac{19\pi}{2}+1$,所以在矩形ABCD内随机取一点,此点取自阴影部分的概率是$\frac{\frac{19\pi}{2}+1}{40}=\frac{19\pi + 2}{80}$.故选D.
16.新课标推理能力「2024 广东广州南沙期末」如图,平行四边形 ABCD 中,AC,BD 是两条对角线,现在从以下四个关系:①$AB = BC$,②$AC = BD$,③$AC\perp BD$,④$AB\perp BC$中随机取出一个作为条件,即可推出平行四边形 ABCD 是矩形的概率为

$\frac{1}{2}$
.
答案:16.答案$\frac{1}{2}$
解析 根据矩形的判定定理,可推出平行四边形ABCD是矩形的有②④,∴随机取出一个作为条件,即可推出平行四边形ABCD是矩形的概率为$\frac{2}{4}=\frac{1}{2}$.