10.如图,点 O 是 $ □ ABCD $ 的对称中心,l 是过点 O 的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小关系是(
一样大
)
A.甲大
B.乙大
C.一样大
D.无法确定
答案:C 由中心对称图形的性质可知,甲、乙两个区域的面积相等,所以针头扎在甲、乙两个区域的可能性一样大.
11.「2025 北京通州期末,」一个不透明的盒子中装有 1 个黑球,2 个白球,这些球除颜色外没有其他区别.随机从盒子中摸出 2 个球,下列事件属于必然事件的是(
B
)
A.摸出的 2 个球中有黑球
B.摸出的 2 个球中有白球
C.摸出的 2 个球都是黑球
D.摸出的 2 个球都是白球
答案:B 由题意知,随机从盒子中摸出2个球,可能摸出1个黑球1个白球或者2个白球,故摸出的2个球中有白球是必然事件,故选B.
12.「」下列事件中,属于确定性事件的有(
B
)
①投掷一枚硬币,正面朝上;
②方程 $ x^{2}-3x - 4 = 0 $ 的两根之积等于 -4;
③经过有红绿灯的十字路口,遇到红灯;
④地球自转;
⑤在篮球比赛中,弱队战胜强队.
A.1 个
B.2 个
C.3 个
D.4 个
答案:B ①投掷一枚硬币,正面朝上,是随机事件;②方程$x^{2}-3x-4=0$的两根之积等于-4,是必然事件,属于确定性事件;③经过有红绿灯的十字路口,遇到红灯,是随机事件;④地球自转,是必然事件,属于确定性事件;⑤在篮球比赛中,弱队战胜强队,是随机事件.故选B.
13.跨电路「」如图,电路图中有 4 个开关 A,B,C,D 和 1 个小灯泡,同时闭合开关 A,B 或同时闭合开关 C,D 都可以使小灯泡发光.下列操作中,会使“小灯泡发光”这个事件是随机事件的是(
B
)
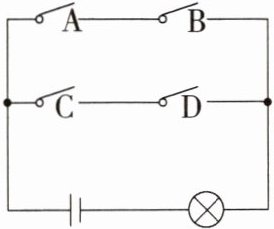
A.只闭合 1 个开关
B.闭合 2 个开关
C.闭合 3 个开关
D.闭合 4 个开关
答案:B 选项A,只闭合1个开关,小灯泡不会发光,属于不可能事件,不符合题意;选项B,闭合2个开关,小灯泡可能发光也可能不发光,是随机事件,符合题意;选项C,闭合3个开关,小灯泡一定发光,是必然事件,不符合题意;选项D,闭合4个开关,小灯泡一定发光,是必然事件,不符合题意.故选B.
14.「2024 广东珠海金湾开学测试,」一个盒子中有红、黄、蓝三种颜色的球共 10 个(每个球的形状、大小都相同),其中红球有 5 个.如果从中任意摸出一个,摸到黄球的可能性比摸到蓝球的可能性大,那么黄球最多有
4
个.如果这些球中只有一个略轻,其他的一样重,用无砝码的天平至少称
3
次可以保证找到这个略轻的球.
答案:答案 4;3
解析 由题意得,盒子中黄球和蓝球共有5个且摸到黄球的可能性比摸到蓝球的可能性大,所以黄球最多有4个.如果这些球中只有一个略轻,其他的一样重,用无砝码的天平至少称3次可以保证找到这个略轻的球.
15.新数据观念 如图,一个转盘被平均分成 12 份,每份写上不同的数字.游戏规则:先猜数,后转动转盘,若指针指向的数字与所猜的数字一致,则猜数者获胜.现提供三种猜数方法:
(1)猜“是奇数”或“是偶数”;
(2)猜“是大于 10 的数”或“是不大于 10 的数”;
(3)猜“是 3 的倍数”或“不是 3 的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?怎样猜?并说明理由.

选择第
(3)
种方法,猜
是3的倍数
.
理由:∵转盘中,奇数与偶数的个数相同,大于10的数与不大于10的数的个数也相同,
∴方法(1)与(2)无论猜哪个,获胜的可能性都为$\frac{1}{2}$.
∵转盘中的数是3的倍数的有7个,不是3的倍数的有5个,
∴猜“是3的倍数”获胜的机会大.
∴选择第(3)种方法,猜“是3的倍数”获胜的机会最大.
答案:解析 选择第(3)种方法,猜“是3的倍数”.
理由:∵转盘中,奇数与偶数的个数相同,大于10的数与不大于10的数的个数也相同,
∴方法(1)与(2)无论猜哪个,获胜的可能性都为$\frac{1}{2}$.
∵转盘中的数是3的倍数的有7个,不是3的倍数的有5个,
∴猜“是3的倍数”获胜的机会大.
∴选择第(3)种方法,猜“是3的倍数”获胜的机会最大.