答案：
D ∵ 四边形 $ABCD$ 是正方形，∴ $∠BCD = 90^{\circ}$，
∵ $∠PDC = ∠PCB$，∴ $∠PDC + ∠PCD = 90^{\circ}$，
∴ $∠DPC = 90^{\circ}$，∴ 点 $P$ 在以 $CD$ 为直径的圆上，
如图，取 $CD$ 的中点 $M$，连接 $AM$，$PM$，则 $M$ 是该圆的圆心，点 $A$ 在 $⊙M$ 外，$CM = DM = 1$，
在 $△APM$ 中，$AP ＞ AM - PM$，∴ 当 $A$，$P$，$M$ 三点共线时，$AP$ 有最小值，此时 $AP = AM - PM = \sqrt{1^{2} + 2^{2}} - 1 = \sqrt{5} - 1$。故选 D。

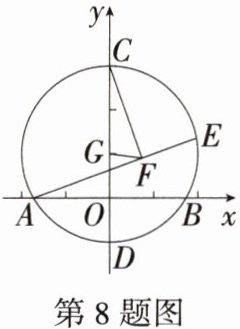
答案：
答案 $2\sqrt{3}$；$\sqrt{3} - 1$
解析 如图，连接 $AG$。∵ $GO⊥AB$，∴ $OA = OB$，在 $Rt△AGO$ 中，∵ $AG = 2$，$OG = 1$，∴ $AG = 2OG$，$OA = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$，∴ $∠GAO = 30^{\circ}$，$AB = 2AO = 2\sqrt{3}$。
连接 $AC$，∵ $OA = \sqrt{3}$，$OC = 3$，∴ $AC = 2\sqrt{3}$。
∵ $CF⊥AE$，∴ 点 $F$ 在以 $AC$ 为直径的圆上，
取 $AC$ 的中点 $M$，连接 $MF$，$MG$，则有 $FG≥FM - GM$，
∵ $GA = GC$，$MA = MC$，∴ $GM$ 垂直平分 $AC$，
∵ $GC = GA$，∴ $∠GCA = ∠GAC = 30^{\circ}$，∴ $MG = \frac{1}{2}AG = 1$，
∵ $M$ 为 $AC$ 中点，$∠CFA = 90^{\circ}$，∴ $FM = \frac{1}{2}AC = \sqrt{3}$，
∴ $FG$ 的最小值为 $FM - GM = \sqrt{3} - 1$。

答案：
答案 $\frac{8}{3}$
解析 ∵ $∠APD = 90^{\circ}$，∴ 点 $P$ 在以线段 $AD$ 的中点 $O$ 为圆心，$AD$ 为直径的圆上，易知当 $EC$ 与圆 $O$ 相切时，$AE$ 的值最大。如图，设 $CE$ 与圆 $O$ 相切于点 $F$，由切线长定理得 $AE = EF$，$CF = CD = 6$，在 $Rt△BCE$ 中，$BE = 6 - AE$，$EC = EF + FC = 6 + AE$，$BC = 8$，由勾股定理得 $(6 - AE)^{2} + 8^{2} = (6 + AE)^{2}$，∴ $AE = \frac{8}{3}$。即 $AE$ 的最大值为 $\frac{8}{3}$。

答案：
答案 $\frac{16\sqrt{3}}{3}$
解析 如图，作 $△ABC$ 的外接圆 $⊙O$，连接 $OA$，$OB$，$OC$，过点 $O$ 作 $OE⊥BC$ 于点 $E$，∵ $∠BAC = 60^{\circ}$，∴ $∠BOC = 120^{\circ}$，∵ $OB = OC$，∴ $∠OBC = ∠OCB = 30^{\circ}$，设 $⊙O$ 的半径为 $r$，则 $OE = \frac{1}{2}OB = \frac{1}{2}r$，$BE = \frac{\sqrt{3}}{2}OB = \frac{\sqrt{3}}{2}r$，∴ $BC = \sqrt{3}r$，∵ $OA + OE≥AD$，∴ $r + \frac{1}{2}r≥4$，解得 $r≥\frac{8}{3}$，∴ $BC≥\frac{8\sqrt{3}}{3}$，∴ $S_{△ABC} = \frac{1}{2}BC·AD≥\frac{1}{2}×\frac{8\sqrt{3}}{3}×4 = \frac{16\sqrt{3}}{3}$，∴ $△ABC$ 面积的最小值为 $\frac{16\sqrt{3}}{3}$。

答案：
答案 $2 - \sqrt{2}$
解析 如图①，∵ $∠MCN = 45^{\circ}$，∴ 在 $AB$ 上方以 $MN$ 为斜边作等腰 $Rt△MON$，作 $△CMN$ 的外接圆 $⊙O$，连接 $OC$，取 $MN$ 的中点 $P$，$AB$ 的中点 $Q$，连接 $OP$、$CP$、$CQ$，设 $⊙O$ 的半径为 $r$，在 $Rt△ABC$ 中，$AC = BC = 1$，∴ $AB = \sqrt{2}$，∴ $CQ = \frac{\sqrt{2}}{2}$，在 $Rt△MON$ 中，$OM = ON = r$，∴ $MN = \sqrt{2}r$，∴ $OP = \frac{\sqrt{2}}{2}r$。∵ $OC + OP≥CP≥CQ$，∴ $r + \frac{\sqrt{2}}{2}r≥CP≥\frac{\sqrt{2}}{2}$。如图②，当且仅当点 $C$、$O$、$P$ 共线，且 $CP$ 与 $CQ$ 重合时，$r + \frac{\sqrt{2}}{2}r = \frac{\sqrt{2}}{2}$，此时 $r$ 最小，解得 $r = \sqrt{2} - 1$，∴ $MN = \sqrt{2}r = 2 - \sqrt{2}$，即 $MN$ 的最小值为 $2 - \sqrt{2}$。

答案：
答案 $4\sqrt{3}$
解析 如图，将 $△ADF$ 绕点 $A$ 顺时针旋转 $120^{\circ}$ 到 $△ABM$，由旋转得 $BM = DF$，$AM = AF$，$∠ABM = ∠D = 120^{\circ}$，$∠MAF = 120^{\circ}$，∵ $∠ABC = 60^{\circ}$，∴ $∠ABM + ∠ABC = 180^{\circ}$，∴ $M$、$B$、$E$ 三点共线，∵ $∠EAF = 60^{\circ}$，∴ $∠MAE = 120^{\circ} - 60^{\circ} = 60^{\circ}$。又 ∵ $AM = AF$，$AE = AE$，∴ $△MAE≌△FAE(SAS)$，∴ $∠MEA = ∠FEA$，过点 $A$ 作 $AH⊥BC$ 于 $H$，作 $AK⊥EF$ 于 $K$，∴ $AH = AK = 2\sqrt{3}$，作 $△AEF$ 的外接圆 $⊙O$，连接 $OA$、$OE$、$OF$，过点 $O$ 作 $ON⊥EF$ 于 $N$，∵ $∠EAF = 60^{\circ}$，∴ $∠EOF = 120^{\circ}$，∴ $∠NOF = 60^{\circ}$，设 $EF = 2x$，则 $NF = x$，在 $Rt△ONF$ 中，易得 $ON = \frac{\sqrt{3}}{3}x$，$OF = \frac{2\sqrt{3}}{3}x$，∴ $ON + OA = ON + OF = \sqrt{3}x$，∵ $OA + ON≥AK$，∴ $\sqrt{3}x≥2\sqrt{3}$，∴ $x≥2$，∴ $S_{△AEF} = \frac{1}{2}EF·AK = \frac{1}{2}×2x×2\sqrt{3} = 2\sqrt{3}x≥4\sqrt{3}$，∴ $△AEF$ 面积的最小值是 $4\sqrt{3}$。