2025年5年中考3年模拟九年级数学上册人教版第84页解析答案

1. 学科多解法 [2024 四川凉山州会东二模]如图,矩形$ABCD的对角线相交于O$,过点$O作OE\perp BD$,交$AD于点E$,连接$BE$,若$\angle ABE= 20^{\circ}$,则$\angle AOE$的大小是( )

A. $10^{\circ}$
B. $15^{\circ}$
C. $20^{\circ}$
D. $30^{\circ}$

答案：
C 【解法一】∵ 四边形 $ABCD$ 是矩形，∴ $∠BAE = 90^{\circ}$，∵ $OE⊥BD$，∴ $∠BOE = 90^{\circ}$，∵ $∠BAE + ∠BOE = 180^{\circ}$，∴ $A$、$B$、$O$、$E$ 四点共圆，∴ $∠AOE = ∠ABE = 20^{\circ}$。故选 C。
【解法二】如图，取 $BE$ 的中点 $K$，连接 $AK$、$OK$，∴ $BK = EK$。
∵ 四边形 $ABCD$ 是矩形，
∴ $∠BAE = 90^{\circ}$，∴ $AK = EK$。
∵ $EO⊥BD$，∴ $∠BOE = 90^{\circ}$，∴ $OK = BK$，
∴ $KA = KB = KO = KE$，∴ $A$、$B$、$O$、$E$ 四点都在 $⊙K$ 上，
∴ $∠AOE = ∠ABE = 20^{\circ}$。故选 C。

2. 如图,已知在扇形$AOB$中,$\angle AOB= 120^{\circ}$,半径$OA= OB= 8$。$P为弧AB$上的动点,过点$P作PM\perp OA于点M$,$PN\perp OB于点N$,点$M$,$N分别在半径OA$,$OB$上,连接$MN$。点$D是\triangle PMN$的外心,则点$D$运动的路径长为______。

答案：
答案 $\frac{4\pi}{3}$
解析如图，连接 $OP$，∵ $PM⊥OA$，$PN⊥OB$，∴ $∠PMO = ∠PNO = 90^{\circ}$，∴ $M$，$O$，$N$，$P$ 四点共圆，且 $OP$ 为所在圆的直径。又 ∵ 点 $D$ 是 $△PMN$ 的外心，∴ $D$ 为 $OP$ 的中点，∴ $OD = \frac{1}{2}OP = \frac{1}{2}OA = 4$。点 $P$ 在弧 $AB$ 上运动，其路径是一段弧，由题意可知，当点 $M$ 与点 $O$ 重合时，$∠PMB = 30^{\circ}$，当点 $N$ 与点 $O$ 重合时，$∠PNA = 30^{\circ}$，∴ 点 $P$ 运动路径所对的圆心角为 $120^{\circ} - 30^{\circ} - 30^{\circ} = 60^{\circ}$，∴ 点 $D$ 在以 $O$ 为圆心，$4$ 为半径的圆上运动，且点 $D$ 运动路径所对的圆心角为 $60^{\circ}$，∴ 点 $D$ 运动的路径长为 $\frac{60\pi×4}{180} = \frac{4}{3}\pi$。

3. 如图,$AB\perp BC$,$AB= 5$,点$E$、$F分别是线段AB$、射线$BC$上的动点,以$EF为斜边作等腰Rt\triangle DEF$,$\angle EDF= 90^{\circ}$,连接$AD$,则$AD$的最小值为______。

答案：
答案 $\frac{5\sqrt{2}}{2}$
解析如图，连接 $BD$ 并延长。∵ $AB⊥BC$，∴ $∠ABC = 90^{\circ}$，又 ∵ $∠EDF = 90^{\circ}$，∴ $B$，$E$，$D$，$F$ 四点共圆。∵ $△DEF$ 为等腰直角三角形，∴ $∠DEF = ∠DFE = 45^{\circ}$，∴ $∠DBF = ∠DEF = 45^{\circ}$，∴ $∠DBF = ∠DBE = 45^{\circ}$，∴ 点 $D$ 在 $∠ABC$ 的平分线上运动，∴ 当 $AD⊥BD$ 时，$AD$ 取最小值，∴ $AD$ 的最小值为 $\frac{\sqrt{2}}{2}AB = \frac{5\sqrt{2}}{2}$。

4. 如图,已知$AB= AC= AD$,$\angle CBD= 44^{\circ}$,则$\angle CAD$的度数为( )

A. $68^{\circ}$
B. $88^{\circ}$
C. $90^{\circ}$
D. $112^{\circ}$

答案：
B ∵ $AB = AC = AD$，∴ $B$，$C$，$D$ 三点在以点 $A$ 为圆心，$AB$ 长为半径的圆上，如图所示，

∵ $∠CBD = 44^{\circ}$，∴ $∠CAD = 2∠CBD = 88^{\circ}$。故选 B。

5. [2024 安徽合肥蜀山期末]如图,点$A$,$B的坐标分别为(2,0)$,$(0,2)$,点$C$为坐标平面内一点,$BC= 1$,点$M为线段AC$的中点,连接$OM$,则$OM$的最大值为( )

A. $\sqrt{2}+\frac{1}{2}$
B. $\sqrt{2}+1$
C. $2\sqrt{2}+1$
D. $2\sqrt{2}-\frac{1}{2}$

答案：
A 以 $B$ 为圆心，$1$ 为半径作 $⊙B$，在 $x$ 轴的负半轴上取一点 $D$，使 $OD = OA = 2$，连接 $CD$，∵ $BC = 1$，∴ 点 $C$ 在 $⊙B$ 上，∵ 点 $M$ 为线段 $AC$ 的中点，∴ $AM = CM$，又 $OD = OA$，∴ $OM$ 是 $△ACD$ 的中位线，∴ $OM = \frac{1}{2}CD$，易知当 $D$，$B$，$C$ 三点共线时，如图，$CD$ 取得最大值，即 $OM$ 取得最大值，∵ $OB = OD = 2$，$∠BOD = 90^{\circ}$，∴ $BD = \sqrt{OB^{2} + OD^{2}} = 2\sqrt{2}$，∴ $CD = 2\sqrt{2} + 1$，∴ $OM = \frac{1}{2}CD = \sqrt{2} + \frac{1}{2}$，∴ $OM$ 的最大值为 $\sqrt{2} + \frac{1}{2}$。故选 A。

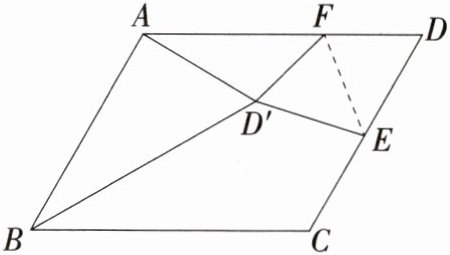
6. [2024 山东烟台中考]如图,在$□ ABCD$中,$\angle C= 120^{\circ}$,$AB= 8$,$BC= 10$,$E为边CD$的中点,$F为边AD$上的一动点,将$\triangle DEF沿EF翻折得\triangle D'EF$,连接$AD'$,$BD'$,则$\triangle ABD'$面积的最小值为______。

答案：
答案 $20\sqrt{3} - 16$
解析由翻折得 $D'E = DE$，
∵ $E$ 是 $CD$ 的中点，∴ $D'E = DE = CE$，
即点 $D'$ 的运动轨迹是以点 $E$ 为圆心，$\frac{1}{2}CD$ 长为半径的圆弧。
如图，过点 $C$ 作 $CG⊥AB$ 于点 $G$，过点 $E$ 作 $EH⊥BA$ 交 $BA$ 的延长线于点 $H$，交圆 $E$ 于 $D'$，则 $HE = CG$，此时 $D'$ 到边 $AB$ 的距离最小，最小值为 $D'H$ 的长，即此时 $△ABD'$ 面积的值最小。

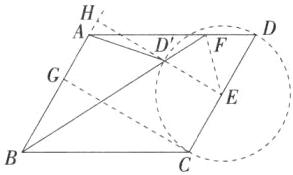
∵ 在 $□ABCD$ 中，$∠BCD = 120^{\circ}$，
∴ $∠ABC = 60^{\circ}$，∴ 在 $Rt△BCG$ 中，$∠BCG = 30^{\circ}$，
∵ $BC = 10$，∴ $CG = 5\sqrt{3}$，∴ $EH = 5\sqrt{3}$，
∵ $CD = AB = 8$，∴ $D'E = DE = 4$，∴ $HD' = 5\sqrt{3} - 4$，
∴ $△ABD'$ 面积的最小值为 $\frac{1}{2}×8×(5\sqrt{3} - 4) = 20\sqrt{3} - 16$。