1.「2024 四川凉山州中考」点 $ P(a,-3) $ 关于原点对称的点是 $ P'(2,b) $,则 $ a + b $ 的值是(
A
)
A. 1
B. -1
C. -5
D. 5
答案:A ∵ 点 $ P(a,-3) $ 关于原点对称的点是 $ P'(2,b) $,∴ $ a = -2 $,$ b = 3 $,∴ $ a + b = 1 $。故选 A。
2. 学习教材变式特色 $ P69 $ 练习 $ T1 $ 在平面直角坐标系中,有 $ A(2,-1) $,$ B(-1,-2) $,$ C(2,1) $,$ D(-2,1) $ 四点. 其中关于原点对称的两点为(
D
)
A. 点 $ A $ 和点 $ B $
B. 点 $ B $ 和点 $ C $
C. 点 $ C $ 和点 $ D $
D. 点 $ D $ 和点 $ A $
答案:D
3.「2025 山东德州德城月考」在平面直角坐标系中,点 $ M(3,-4) $ 关于原点对称的点为 $ N $,连接 $ MN $,则线段 $ MN $ 的长是( )
A. 6
B. 8
C. 10
D. 12
答案:C ∵ 点 $ M(3,-4) $ 关于原点的对称点为点 $ N $,∴ 点 $ N(-3,4) $,如图,过点 $ M $ 作 $ MA \perp x $ 轴于点 $ A $,在 $ \text{Rt} \triangle AOM $ 中,$ OA = 3 $,$ AM = 4 $,∴ $ OM = \sqrt{OA^{2} + AM^{2}} = 5 $,由中心对称的性质可知,$ MN = 2OM = 10 $。故选 C。

4.「2025 湖北荆州松滋期中」在平面直角坐标系中,$ \triangle ABO $ 的三个顶点坐标分别为 $ A(2,3) $、$ B(3,1) $、$ O(0,0) $.
(1) 将 $ \triangle ABO $ 向右平移 4 个单位,画出平移后的 $ \triangle A_1B_1O_1 $.
(2) 以点 $ O $ 为对称中心,画出与 $ \triangle ABO $ 成中心对称的 $ \triangle A_2B_2O $.
(3) 直接写出四边形 $ ABA_2B_2 $ 的面积:______.
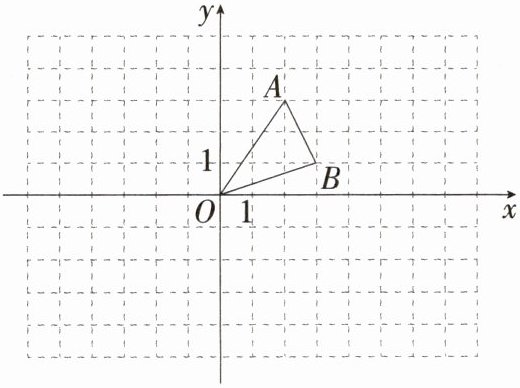
答案:解析 (1) 如图,$ \triangle A_{1}B_{1}O_{1} $ 即为所求作的三角形。
(2) 如图,$ \triangle A_{2}B_{2}O $ 即为所求作的三角形。

(3) 14.
提示:取 $ C(3,3) $,$ D(3,-3) $,$ F(-3,-3) $,$ E(-3,3) $ 四点,依次连接点 $ C $、$ D $、$ F $、$ E $,得到正方形 $ CDFE $,∴ 四边形 $ ABA_{2}B_{2} $ 的面积 $ = S_{\text{正方形} CDFE} - 2S_{\triangle ABC} - 2S_{\triangle BDA_{1}} = 6 \times 6 - 2 \times \frac{1}{2} \times 1 \times 2 - 2 \times \frac{1}{2} \times 4 \times 5 = 14 $。
5.「2025 云南昆明期末,★☆」已知 $ \sqrt{(a - 2)^2} + |b + 1| = 0 $,则点 $ P(a,b) $ 关于原点对称的点的坐标是(
C
)
A. $ (2,-1) $
B. $ (-2,-1) $
C. $ (-2,1) $
D. $ (2,1) $
答案:C ∵ $ \sqrt{(a - 2)^{2}} + |b + 1| = 0 $,∴ $ a - 2 = 0 $,$ b + 1 = 0 $,∴ $ a = 2 $,$ b = -1 $,∴ 点 $ P(2,-1) $,则点 $ P(2,-1) $ 关于原点对称的点的坐标为 $ (-2,1) $。故选 C。
6.「2024 河北保定顺平期中,★☆」若点 $ P(a + 1,a - 2) $ 关于原点对称的点位于第一象限,则 $ a $ 的取值范围用数轴表示正确的是(
B
)

答案:B ∵ 点 $ P(a + 1,a - 2) $ 关于原点对称的点在第一象限,∴ 点 $ P $ 在第三象限,∴ $ a + 1 < 0 $,$ a - 2 < 0 $,解得 $ a < -1 $。故选 B。
7.「2024 陕西中考,★☆」一个正比例函数的图象经过点 $ A(2,m) $ 和点 $ B(n,-6) $. 若点 $ A $ 与点 $ B $ 关于原点对称,则这个正比例函数的表达式为(
A
)
A. $ y = 3x $
B. $ y = -3x $
C. $ y = \frac{1}{3}x $
D. $ y = -\frac{1}{3}x $
答案:A ∵ 点 $ A(2,m) $ 和点 $ B(n,-6) $ 关于原点对称,∴ $ m = 6 $,∴ 点 $ A $ 的坐标为 $ (2,6) $。设正比例函数的表达式为 $ y = kx(k \neq 0) $,∵ 点 $ A(2,6) $ 在正比例函数 $ y = kx $ 的图象上,∴ $ 6 = 2k $,解得 $ k = 3 $,∴ 正比例函数的表达式为 $ y = 3x $。故选 A。
8.「2025 甘肃武威凉州期中,★☆」若方程 $ x^2 + mx + n = 0 $ 的两根分别为 $ x_1 = -5 $,$ x_2 = 3 $,则点 $ P(m,n) $ 关于原点对称的点的坐标是
(-2,15)
.
答案:答案 $ (-2,15) $
解析 ∵ 方程 $ x^{2} + mx + n = 0 $ 的两根分别为 $ x_{1} = -5 $,$ x_{2} = 3 $,∴ $ x_{1} + x_{2} = -m = -5 + 3 = -2 $,$ x_{1} \cdot x_{2} = n = (-5) \times 3 = -15 $,∴ $ m = 2 $,∴ $ P(2,-15) $,∴ 点 $ P(2,-15) $ 关于原点对称的点的坐标为 $ (-2,15) $。
9. 新 课标 空间观念「2024 河南南阳淅川期中」在平面直角坐标系中,点 $ A(-5,-1) $ 关于原点对称的点 $ A' $ 的坐标为 $ (a,b) $,关于 $ x $ 轴对称的点 $ B $ 的坐标为 $ (c,d) $,则一次函数 $ y = (a - c)x - (b + d) $ 的图象不经过的象限是(
B
)
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:B ∵ $ A(-5,-1) $,∴ 点 $ A $ 关于原点对称的点 $ A' $ 的坐标为 $ (5,1) $,关于 $ x $ 轴对称的点 $ B $ 的坐标为 $ (-5,1) $,∴ $ a = 5 $,$ b = 1 $,$ c = -5 $,$ d = 1 $,∴ $ a - c = 10 $,$ b + d = 2 $,∴ 一次函数为 $ y = 10x - 2 $,∴ 一次函数图象不经过第二象限。故选 B。
10. 新 课标 运算能力「2024 四川绵阳三模」若点 $ A(1,m) $ 与点 $ B(-1,1 - |x|) $ 关于原点 $ O $ 成中心对称,则 $ m $ 的最小值为______
-1
.
答案:答案 $ -1 $
解析 ∵ 点 $ A(1,m) $ 与点 $ B(-1,1 - |x|) $ 关于原点 $ O $ 成中心对称,∴ $ m + 1 - |x| = 0 $,∴ $ m = |x| - 1 $,∵ $ |x| \geq 0 $,∴ 当 $ |x| = 0 $ 时,$ m $ 的值最小,最小值为 $ -1 $。