2025年5年中考3年模拟九年级数学上册人教版第37页解析答案

6. [2024天津和平月考]如图,要围一个矩形菜园ABCD,其中一边AD靠墙,且AD的长不能超过26m,其余的三边AB,BC,CD用篱笆围成,且这三边的和为40m,有下列结论：
①AB的长可以为6m；
②AB的长有两个不同的值满足菜园ABCD的面积为$192m^2$的条件；
③菜园ABCD面积的最大值为$210m^2.$
其中,正确结论的个数是(

)

A.0
B.1
C.2
D.3

答案：6.B　设AD的长为x m，则AB的长为$\frac{40 - x}{2}m$，当AB = 6m时，$\frac{40 - x}{2}=6$，解得x = 28，∵AD的长不能超过26m，∴x≤26，故①错误.∵菜园ABCD的面积为192m²，∴$x\cdot\frac{40 - x}{2}=192$，整理，得x² - 40x + 384 = 0，解得x = 24或x = 16，∴AB的长有两个不同的值满足菜园ABCD的面积为192m²的条件，故②正确.设矩形菜园的面积为y m²，根据题意，得$y=x\cdot\frac{40 - x}{2}=-\frac{1}{2}(x^{2}-40x)=-\frac{1}{2}(x - 20)^{2}+200$，∵$-\frac{1}{2}＜0$，20 ＜ 26，∴当x = 20时，y有最大值，为200，故③错误.故正确的结论有1个.故选B.

7. [2025安徽亳州利辛期中]九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,如图,最佳方案是( )

A.方案1
B.方案2
C.方案3
D.三个方案都是最佳方案

答案：
7.C　方案1:设矩形的面积为S平方米，垂直于墙的一边长为x米，则平行于墙的一边长为(8 - 2x)米，则S = x(8 - 2x)=-2(x - 2)² + 8，∴当x = 2时，菜园面积有最大值，为8平方米;
方案2:如图，设等腰三角形为△ABC，其中AB = AC = 4米，作BH⊥AC交AC于H，由题意可得BH≤AB，即BH≤4米，∵△ABC的面积$=\frac{1}{2}AC\cdot BH$，∴当BH = 4米时，菜园面积有最大值，为$\frac{1}{2}\times4\times4 = 8$(平方米);

方案3:半圆的半径为$\frac{8}{\pi}$米，此时菜园的面积为$\frac{1}{2}\pi\times(\frac{8}{\pi})^{2}=\frac{32}{\pi}$(平方米).∵$\frac{32}{\pi}＞8$，∴方案3是最佳方案.故选C.

8. [2024广东韶关仁化期末]某校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,墙的最大可用长度为12米.其余三边用总长为26米的木板材料围成.车棚形状如图1(矩形ABCD).为了方便学生出行,学校决定在与墙平行的一边开一个2米宽的门.
(1)求这个车棚的最大面积,此时AB与AD的长分别为多少米.
最大面积为

平方米，此时AB为

米，AD为

米.
(2)如图2,在(1)的结论下,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为70平方米,那么小路的宽度是多少米？
小路的宽度是

米.

答案：8.解析　(1)设车棚的面积为S平方米，垂直于墙的边AB = x米，则平行于墙的边BC = (26 - 2x + 2)米，则S = x(28 - 2x)=-2x² + 28x=-2(x - 7)² + 98，由题意得26 - 2x + 2≤12，26 - 2x＞0，∴8≤x＜13，∴当x = 8时，S有最大值，此时AB = 8米，AD = 12米，面积为96平方米.
(2)设小路的宽度为a米，由(1)知车棚的最大面积为96平方米，AB = 8米，AD = 12米，当停放自行车的面积为70平方米时，小路的占地面积为96 - 70 = 26(平方米)，∴2×8a + 12a - 2a² = 26，解得a = 1或a = 13(不合题意，舍去).
答:小路的宽度为1米.

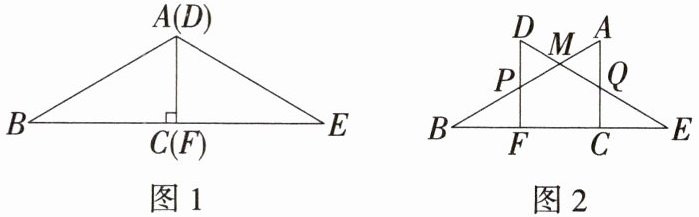
9. 如图1,放置两个全等的含有30°角的直角三角尺ABC与DEF(∠B= ∠E= 30°).若将三角尺ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止),移动过程中始终保持点B,F,C,E在同一条直线上,如图2,AB与DF,DE分别交于点P,M,AC与DE交于点Q,其中AC= DF= √3,设三角尺ABC的移动时间为x秒.
(1)在移动过程中,试用含x的代数式表示△AMQ的面积.
(2)当x等于多少时,两个三角尺重叠部分的面积有最大值？最大值是多少？

答案：
9.解析　(1)∵在Rt△ABC中，∠B = 30°，∴∠A = 60°.
∵∠E = 30°，∴∠EQC = ∠AQM = 60°，
∴△AMQ为等边三角形，
如图，过点M作MN⊥AQ，垂足为N.

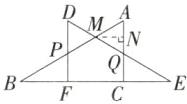
在Rt△ABC中，∠B = 30°，AC = $\sqrt{3}$，则BC = 3，
∴EF = BC = 3.根据题意知CF = x，
∴CE = EF - CF = 3 - x，易得$CQ=\frac{\sqrt{3}}{3}(3 - x)$，
∴$AQ=AC - CQ=\sqrt{3}-\frac{\sqrt{3}}{3}(3 - x)=\frac{\sqrt{3}}{3}x$，
∴$AM=AQ=\frac{\sqrt{3}}{3}x$，∴$MN=\frac{1}{2}x$，
∴$S_{\triangle AMQ}=\frac{1}{2}AQ\cdot MN=\frac{1}{2}\times\frac{\sqrt{3}}{3}x\cdot\frac{1}{2}x=\frac{\sqrt{3}}{12}x^{2}$.
(2)由(1)知BF = CE = 3 - x，$PF=\frac{\sqrt{3}}{3}(3 - x)$，
设两个三角尺重叠部分的面积为$S_{重叠}$，
∴$S_{重叠}=S_{\triangle ABC}-S_{\triangle AMQ}-S_{\triangle BPF}=\frac{1}{2}AC\cdot BC - S_{\triangle AMQ}-\frac{1}{2}BF\cdot PF=\frac{1}{2}\times\sqrt{3}\times3-\frac{\sqrt{3}}{12}x^{2}-\frac{1}{2}(3 - x)\cdot\frac{\sqrt{3}}{3}(3 - x)=-\frac{\sqrt{3}}{4}x^{2}+\sqrt{3}x=-\frac{\sqrt{3}}{4}(x - 2)^{2}+\sqrt{3}$，
∴当x = 2时，重叠部分面积有最大值，最大值是$\sqrt{3}$.