2025年5年中考3年模拟九年级数学上册人教版第101页解析答案

1.「2024 内蒙古通辽中考」手工课堂上,老师给每个制作小组发

放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.

【模型建立】
(1)如图 1,从花折伞中抽象出“牵形图”,$AM = AN$,$DM = DN$.求证$∠AMD = ∠AND$.
【模型应用】
(2)如图 2,在$△AMC$中,$∠MAC的平分线AD交MC于点D$.请你从以下两个条件：①$∠AMD = 2∠C$；②$AC = AM + MD$中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注：只需选择一种情况作答)
【拓展提升】
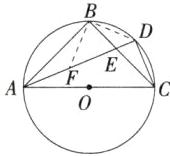
(3)如图 3,$AC为\odot O$的直径,$\overset{\frown}{AB} = \overset{\frown}{BC}$,$∠BAC的平分线AD交BC于点E$,交$\odot O于点D$,连接$CD$.求证：$AE = 2CD$.

答案：
解析
(1) 证明：在$\triangle ADM$和$\triangle ADN$中，$\left\{\begin{array}{l} AM = AN,\\ DM = DN,\\ AD = AD,\end{array}\right.$
$\therefore \triangle ADM\cong \triangle ADN(SSS)$，
$\therefore ∠AMD = ∠AND$。
(2) 选择②为条件，①为结论，
如图，在$AC$上取点$N$，使$AN = AM$，连接$DN$，

$\because AD$平分$∠MAC$，$\therefore ∠DAM = ∠DAN$，
在$\triangle ADM$和$\triangle ADN$中，
$\because AM = AN$，$∠DAM = ∠DAN$，$AD = AD$，
$\therefore \triangle ADM\cong \triangle ADN(SAS)$，
$\therefore DM = DN$，$∠AMD = ∠AND$，
$\because AC = AM + MD$，$AC = AN + NC$，
$\therefore DM = CN$，$\therefore DN = CN$，$\therefore ∠C = ∠CDN$，
$\therefore ∠AMD = ∠AND = ∠CDN + ∠C = 2∠C$。
(亦可选择①为条件，②为结论，证明略)
(3) 证明：如图，连接$BD$，取$AE$的中点$F$，连接$BF$，

$\because AD$平分$∠BAC$，$\therefore ∠BAD = ∠DAC$，$\therefore \overset{\frown}{DC} = \overset{\frown}{BD}$，
$\therefore BD = CD$，$\therefore ∠BCD = ∠CBD$，$\because AC$为$\odot O$的直径，
$\therefore ∠ABC = 90^{\circ}$，$\therefore AE = 2BF = 2AF$，$\therefore ∠ABF = ∠BAF$，
$\because ∠BAF = ∠BCD$，$\therefore ∠ABF = ∠CBD$，$\because \overset{\frown}{AB} = \overset{\frown}{BC}$，
$\therefore AB = BC$，$\therefore \triangle ABF\cong \triangle CBD(ASA)$，$\therefore BF = BD = CD$，
$\therefore AE = 2CD$。

2.「2024 广东中考」综合与实践.
【主题】滤纸与漏斗
【素材】如图 1 所示：
①一张直径为 10 cm 的圆形滤纸；
②一只漏斗口直径与母线均为 7 cm 的圆锥形过滤漏斗.

【实践操作】
步骤 1：取一张滤纸；
步骤 2：按如图 2 所示步骤折叠好滤纸；
步骤 3：将其中一层撑开,围成圆锥形；
步骤 4：将围成圆锥形的滤纸放入如图 1 所示漏斗中.

【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)? 用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留$π$)

答案：
解析
(1) 滤纸能紧贴此漏斗内壁。
由$2\pi r=\frac{n\pi l}{180}$得$\frac{n}{360}=\frac{r}{l}$，其中$r$为圆锥底面半径，$l$为圆锥的母线长，$n^{\circ}$为圆锥侧面展开图的圆心角的度数。对于圆锥形滤纸，$n_{1}=90×2 = 180$；对于漏斗，$\frac{r}{l}=\frac{3.5}{7}=\frac{1}{2}$，$\therefore n_{2}=180$。$\because n_{1}=n_{2}$，$\therefore$滤纸能紧贴此漏斗内壁。
(2) 作出示意图如下，由题意知$CD = CE=\frac{1}{2}×10 = 5cm$，$\because$圆锥形的滤纸的底面周长$=\frac{1}{2}×10\pi = 5\pi(cm)$，$\therefore DE = 5cm$，$\therefore CD = DE = CE = 5cm$，$\therefore ∠CDE = 60^{\circ}$，过$C$作$CF⊥DE$于点$F$，则$DF=\frac{1}{2}DE=\frac{5}{2}cm$，在$Rt\triangle CDF$中，$CF=\sqrt{CD^{2}-DF^{2}}=\frac{5\sqrt{3}}{2}cm$，$\therefore$滤纸围成圆锥形的体积是$\pi×(\frac{5}{2})^{2}×\frac{5\sqrt{3}}{2}×\frac{1}{3}=\frac{125\sqrt{3}}{24}\pi cm^{3}$。