3. 甲、乙两辆车同时从A、B两地出发,相向开出,甲车每小时行60千米,乙车每小时比甲车多行$\frac{1}{4}$,经过$\frac{8}{5}$小时两车相遇。A、B两地相距多少千米?
答案:3. 60×(1+$\frac{1}{4}$)=75(千米/时)
(60+75)×$\frac{8}{5}$=216(千米) [提示]先求出乙车的速度,再根据“总路程=速度和×相遇时间”,求出A、B两地的距离。
例4
学校买回一批篮球,按3:4:5分配给低年级、中年级和高年级。已知中年级分到了24个篮球,则低年级和高年级各分到了多少个?
答案:方法一:24÷4=6(个)
低年级:6×3=18(个)
高年级:6×5=30(个)
方法二:24÷$\frac{4}{3+4+5}$=72(个)
低年级:72×$\frac{3}{3+4+5}$=18(个)
高年级:72×$\frac{5}{3+4+5}$=30(个)
答:低年级分到18个,高年级分到30个。
4. 学校买回一批篮球,按3:4:5分给低年级、中年级和高年级。已知高年级比低年级多分得24个,则这批篮球一共有多少个?
答案:4. 24÷$\frac{5-3}{3+4+5}$=144(个) [提示]把篮球的总个数看作单位“1”,用24除以对应的分率$\frac{5-3}{3+4+5}$,即可求出这批篮球的个数。
解析:
24÷$\frac{5-3}{3+4+5}$=144(个)
例5
求涂色部分的面积。(单位:cm)
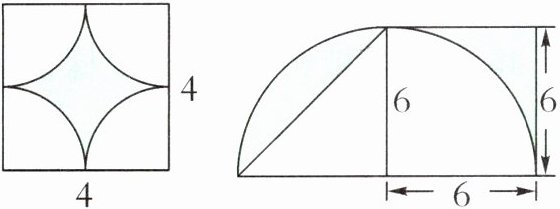
答案:左图:
半径 $r = 4 ÷ 2 = 2$($cm$)。
圆的面积 $= π r^2 = 3.14 × 2^2 = 12.56$($cm^2$)。
正方形面积 $= 4 × 4 = 16$($cm^2$)。
涂色部分面积 $= 16 - 12.56 = 3.44$($cm^2$)。
右图:
正方形面积 $= 6 × 6 = 36$($cm^2$)。
涂色部分面积 $= 36 ÷ 2 = 18$($cm^2$)。
左图涂色部分面积3.44$cm^2$,右图涂色部分面积18$cm^2$。
5. 求下面图形中涂色部分的面积。
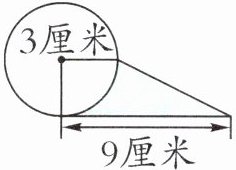
答案:5. (3+9)×3÷2-3.14×3²÷4=10.935(平方厘米)
[提示]题图中涂色部分可以看作是用上底是3厘米、下底是9厘米、高是3厘米的梯形的面积减去半径是3厘米的圆面积的$\frac{1}{4}$。