1. 两个数相乘,一个乘数乘3,另一个乘数也乘3,所得的积比原来增加了560,原来的积是多少?
答案:1. 3×3=9 560÷(9−1)=70
【提示】两个数相乘,一个乘数乘 3,另一个乘数也乘 3,则积乘 9,比原来的积增加了 9−1=8 倍。560 相当于原来积的 8 倍,用 560÷8 即可求出原来的积。
例2从上海到宁波的某列高铁有三种不同的票价,商务座444元/张、一等座237元/张、二等座144元/张。李叔叔买了4张同样价格的车票,付给售票员10张100元的纸币,他买的是(
)。
答案:思路分析
根据“单价×数量=总价”,分别求出三种票各买4张需要的钱数,再与$10×100=1000$(元)比较即可。生活中的问题要注意符合实际。
解答:一等座
归纳点拨
解决此类实际问题时要分析比较,从而找出符合题意的答案。
2. 东山居委会开展公益活动,居委会工作人员要给社区老人买12个同样的热水壶,李主任带了2000元,要使剩余的钱尽量少,应该买哪一种热水壶?剩余多少元?
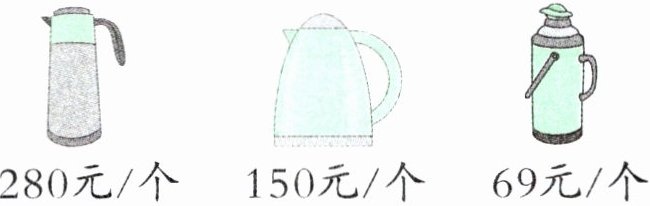
答案:2. 280×12=3360(元)
150×12=1800(元)
69×12=828(元)
828<1800<2000<3360
2000−1800=200(元)
应该买第二种热水壶,剩余 200 元。
【提示】购买第一种热水壶总价超过 2000 元,购买第三种剩余的钱比较多,购买第二种符合题意。
例小华在做三位数乘两位数的计算题时,把第二个乘数14错当作41,乘得的结果是4920。正确的积应该是多少?
答案:思路分析
因为“把第二个乘数14错当作41,乘得的结果是4920”,所以第一个乘数为$4920÷41=120$,用120乘正确的第二个乘数即可。
解答:$4920÷41×14=1680$
归纳点拨
本题考查逆向思维与顺向思维的综合运用能力。在解决“计算错误”这类题目时,做到认真分析算式各部分相对应的变化关系,选择相应的解决办法,就能“错中求解”。
乐乐在做一道三位数乘两位数的计算题时,把第二个乘数25错看成了52,结果比正确的积多了3348。正确的积应该是(
3100
)。
答案:[附加题兴趣班]
3100 【提示】根据“把第二个乘数 25 错看成了 52,结果比正确的积多了 3348”可知,第一个乘数是 3348÷(52−25)=124,则正确的积应该是 124×25=3100。