例 1
从四边形 4 个内角中任取 2 个求和,共有 6 种情况,其中大于 $180^{\circ}$ 的和最多有多少种?
解析
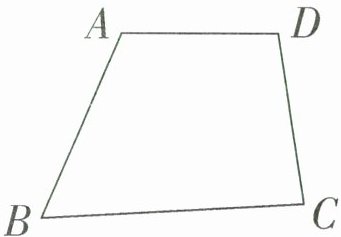
如右图,设四个角分别是 $∠ A$、$∠ B$、$∠ C$、$∠ D$,则 $∠ A+∠ B+∠ C+∠ D=360^{\circ}$,6 个和分别为:$∠ A+∠ B$,$∠ A+∠ C$,$∠ A+∠ D$,$∠ B+∠ C$,$∠ B+∠ D$,$∠ C+∠ D$。可以分三组讨论:
(1)$∠ A+∠ B$ 和 $∠ C+∠ D$,若 $∠ A+∠ B>180^{\circ}$,则 $∠ C+∠ D<180^{\circ}$;
(2)$∠ A+∠ C$ 和 $∠ B+∠ D$,若 $∠ A+∠ C>180^{\circ}$,则 $∠ B+∠ D<180^{\circ}$;
(3)$∠ A+∠ D$ 和 $∠ B+∠ C$,若 $∠ A+∠ D>180^{\circ}$,则 $∠ B+∠ C<180^{\circ}$,所以大于 $180^{\circ}$ 的和最多有 3 种。
答案
大于 $180^{\circ}$ 的和最多有 3 种。
小结
列举所有情况,然后分组讨论,是研究数学问题的一种常用方式。
答案:设四边形的四个内角分别为 $∠A$、$∠B$、$∠C$、$∠D$,则:
$∠A + ∠B + ∠C + ∠D = 360°$。
从四个内角中任取两个角求和,共有以下 6 种组合:
$∠A + ∠B$,
$∠A + ∠C$,
$∠A + ∠D$,
$∠B + ∠C$,
$∠B + ∠D$,
$∠C + ∠D$,
将这些组合分成三组进行讨论:
第1组:$∠A + ∠B$ 和 $∠C + ∠D$
如果 $∠A + ∠B > 180°$,则 $∠C + ∠D = 360° - (∠A + ∠B) < 180°$。
第2组:$∠A + ∠C$ 和 $∠B + ∠D$
如果 $∠A + ∠C > 180°$,则 $∠B + ∠D = 360° - (∠A + ∠C) < 180°$。
第3组:$∠A + ∠D$ 和 $∠B + ∠C$
如果 $∠A + ∠D > 180°$,则 $∠B + ∠C = 360° - (∠A + ∠D) < 180°$。
由以上三组讨论可知,在每一组中,至多只有一个组合的和大于 $180°$。
因此,所有 6 种组合中,大于 $180°$ 的和最多有 3 种。
大于 $180°$ 的和最多有 $3$ 种。
例 2
如果两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由(
)拼成。
A. 两个锐角三角形
B. 两个直角三角形
C. 两个钝角三角形
D. 一个锐角三角形和一个钝角三角形
解析
因为拼在一起的两个小三角形一定有两条边重合,这时能组成一个平角,即 $180^{\circ}$。
A. 因为两个锐角的和小于 $180^{\circ}$,所以两个锐角三角形不可能拼成一个大三角形。
B. 因为 $90^{\circ}+90^{\circ}=180^{\circ}$,所以两个直角三角形能拼成一个大三角形。
C. 因为钝角+锐角有可能等于 $180^{\circ}$,所以两个钝角三角形可能拼成一个大三角形。
D. 因为钝角+锐角有可能等于 $180^{\circ}$,所以一个锐角三角形和一个钝角三角形可能拼成一个大三角形。
答案
A
小结
结合平角 $=180^{\circ}$,列举两个角度数的可能性,可以顺利解决问题。
答案:A
解析:
因为两个小三角形拼成大三角形时,拼合处两条边所夹角之和需为$180^{\circ}$。
选项A,锐角三角形三个角都小于$90^{\circ}$,两个锐角相加小于$180^{\circ}$,所以两个锐角三角形不可能拼成一个大三角形。
选项B,两个直角三角形,直角为$90^{\circ}$,$90^{\circ}+90^{\circ}=180^{\circ}$,可以拼成大三角形。
选项C,钝角三角形有一个角大于$90^{\circ}$,另一个钝角三角形中与之拼合的角为锐角时,有可能和为$180^{\circ}$,所以可能拼成大三角形。
选项D,一个锐角三角形中的角与一个钝角三角形中的角,有可能和为$180^{\circ}$,所以可能拼成大三角形。
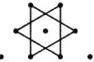
如右图,木板上有 10 根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出(
15
)个等边三角形。

答案:15 【提示】若相邻两根钉子间的距离为 1,则套出的等边三角形中,边长为 1 的等边三角形有 9 个,边长为 2 的等边三角形有 3 个,边长为 3 的等边三角形有 1 个,还有如图的 2 个等边三角形:
。