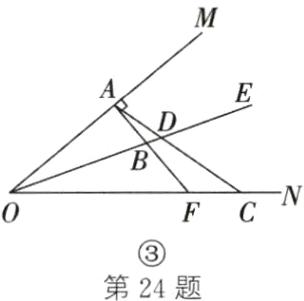
24. (10分)已知∠MON = 40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(点A,B,C不与点O重合),连接AB,AC,AC交射线OE于点D,设∠BAC = α。
(1)如图①,若AB//ON。
① ∠ABO的度数是
20°
。
② 当∠BAD = ∠ABD时,∠OAC的度数是
120°
;当∠BAD = ∠BDA时,∠OAC的度数是
60°
。
(2)在一个四边形中,若存在一个内角是它的对角的2倍,我们称这样的四边形为“完美四边形”。如图②,若AB⊥OM,延长AB交射线ON于点F,当四边形DCFB为“完美四边形”时,求α的值。
答案:24.(1)①20° ②120° 60° (2)
∵OE平分∠MON,∠MON=40°,
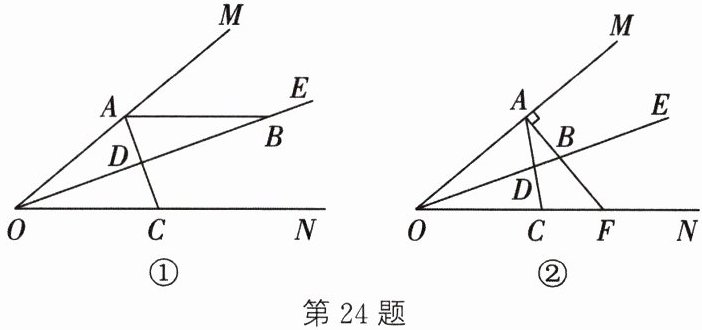
∴∠MOE=∠NOE=$\frac{1}{2}$∠MON=20°.情况1:当∠BDC=2∠BFC时,如图①.
∵AB⊥OM,即∠OAB=90°,∠MON=40°,
∴∠BFC=50°,
∴∠BDC=2∠BFC=100°.
∵∠ABO=∠BFC+∠BON=50°+20°=70°,
∴∠BAC=∠BDC-∠ABO=100°-70°=30°,此时α=30°.情况2:当点C在点F的左边,∠DBF=2∠DCF时,如图②.
∵AB⊥OM,即∠OAB=90°,∠AOB=20°,∠MON=40°,
∴∠DBF=∠AOB+∠OAB=20°+90°=110°,∠BFC=50°,
∴∠DCF=$\frac{1}{2}$∠DBF=55°,
∴∠BAC=180°-∠BFC-∠ACF=180°-50°-55°=75°,此时α=75°.情况3:当点C在点F的右边,∠DBF=2∠DCF时,如图③.
∵AB⊥OM,即∠OAB=90°,∠AOB=20°,∠MON=40°,
∴∠DBF=∠ABO=90°-∠AOB=90°-20°=70°,∠AFO=50°,
∴∠DCF=$\frac{1}{2}$∠DBF=35°,∠AFC=130°,
∴∠BAC=180°-∠DCF-∠AFC=180°-35°-130°=15°,此时α=15°.综上所述,当四边形DCFB为“完美四边形”时,α=30°或75°或15°