16. 如图,$\triangle ABC$ 与 $\triangle BCD$ 都是等边三角形. 有下列说法:① $\triangle BCD$ 可由 $\triangle ABC$ 绕点 $B$ 顺时针旋转 $60^{\circ}$ 得到,$A$ 与 $D$ 是一组对应点;② $\triangle BCD$ 可由 $\triangle ABC$ 绕点 $C$ 逆时针旋转 $60^{\circ}$ 得到,$B$ 与 $D$ 是一组对应点;③ $\triangle BCD$ 可由 $\triangle ABC$ 绕 $BC$ 的中点旋转 $180^{\circ}$ 得到,$B$ 与 $C$ 是一组对应点;④ $\triangle BCD$ 可由 $\triangle ABC$ 关于 $BC$ 作轴对称变换得到,$B$ 与 $C$ 是一组对应点. 其中,正确的有
②③
(填序号).
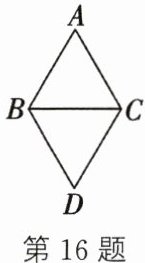
解析:
证明:①假设$\triangle BCD$由$\triangle ABC$绕点$B$顺时针旋转$60°$得到,$A$对应$D$,则$BA=BD$,$\angle ABD=60°$。但$\triangle ABC$是等边三角形,$BA=BC$,若$BD=BA=BC$,则$D$与$C$重合,与图中$D$位置矛盾,①错误。
②$\triangle ABC$与$\triangle BCD$均为等边三角形,$BC=BC$,$AC=CD$,$\angle ACB=\angle BCD=60°$。绕点$C$逆时针旋转$60°$,$A$对应$D$,$B$对应$B$,$\triangle ABC$与$\triangle BCD$重合,②正确。
③设$BC$中点为$O$,则$BO=CO$。绕$O$旋转$180°$,$B$与$C$互换,$A$与$D$关于$O$中心对称,$\triangle ABC$与$\triangle BCD$重合,③正确。
④关于$BC$轴对称,$A$与$D$应关于$BC$对称,此时$AB=BD$,$AC=CD$,但$\angle ABC=\angle DBC=60°$,则$D$在$AB$延长线上,与图中$D$位置不符,④错误。
正确的有②③。
②③