2026年通城学典课时作业本七年级数学下册苏科版江苏专版第51页解析答案

6. 如图，$ \triangle ABC $ 与 $ \triangle A'B'C' $ 关于点 $ O $ 成中心对称，则下列结论不一定成立的是(

)

A.$ A' $ 是点 $ A $ 关于点 $ O $ 的对称点
B.$ BO = B'O $
C.$ AB // A'B' $
D.$ \angle ABC = \angle C'A'B' $

答案：6.D

7. 如图，直线 $ a $，$ b $ 互相垂直且相交于点 $ O $，曲线 $ C $ 关于点 $ O $ 中心对称，点 $ A $ 的对称点是 $ A' $，$ AB ⊥ $ 直线 $ a $ 于点 $ B $，$ A'D ⊥ $ 直线 $ b $ 于点 $ D $.若 $ OB = 3 $，$ OD = 2 $，则涂色部分的面积之和为

答案：7.6

解析：

解：设曲线$C$与$OA$、$OA'$围成的非阴影部分面积分别为$S_1$、$S_2$。
因为曲线$C$关于点$O$中心对称，所以$S_1 = S_2$。
$AB ⊥ a$，$OB = 3$，则$AB$为点$A$到$a$轴的距离；$A'D ⊥ b$，$OD = 2$，则$A'D$为点$A'$到$b$轴的距离。
由中心对称性质，点$A$的横、纵坐标与$A'$的横、纵坐标绝对值相等，设$A$点坐标为$(x,y)$，则$A'$点坐标为$(-x,-y)$，所以$AB = |y|$，$A'D = |x| = 2$，$OB = |x| = 3$（此处应为$OB$是点$A$的横坐标的绝对值，即$|x| = 3$，$OD$是点$A'$的纵坐标的绝对值，即$|y| = 2$）。
矩形$OBAD$（假设构造辅助矩形）面积为$OB × OD = 3×2 = 6$，而涂色部分面积之和等于该矩形面积，即$6$。
6

8. 如图所示为两张完全重合在一起的等边三角形硬纸片，点 $ O $ 是它们的中心.若按住下面的硬纸片不动，将上面的硬纸片绕点 $ O $ 按顺时针方向旋转，则旋转的角度至少为

60°

时，两张硬纸片所构成的图形是中心对称图形.

答案：
8.60°　解析:如图，至少旋转60°，两张硬纸片所构成的图形是中心对称图形.
　　　　　　　　　　

9. 在正方形网格中，$ \triangle ABC $ 的顶点在格点上.请仅用无刻度的直尺完成以下作图.
(1) 如图①，作 $ \triangle ABC $ 关于点 $ O $ 对称的 $ \triangle A'B'C' $；
(2) 如图②，作 $ \triangle ABC $ 绕点 $ A $ 按顺时针方向旋转一定角度后，顶点仍在格点上的 $ \triangle AB''C'' $.

答案：
9.(1)如图①，△A′B′C′即为所求 (2)如图②，△AB″C″即为所求
　　　　　

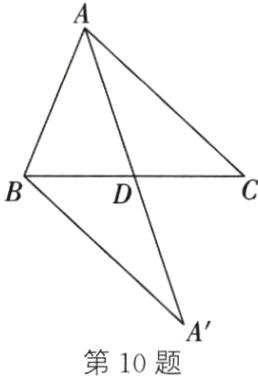
10. 如图，在 $ \triangle ABC $ 中，$ D $ 是边 $ BC $ 的中点，连接 $ AD $.
(1) 画出与 $ \triangle ACD $ 关于点 $ D $ 成中心对称的三角形；
(2) 在(1)的基础上找出与 $ AC $ 相等的线段；
(3) 在 $ \triangle ABC $ 中，探索 $ AB + AC $ 与 $ AD $ 之间的数量关系，并说明理由.

答案：
10.(1)如图，延长AD至点A′，使A′D=AD，连接A′B，则△A′BD就是与△ACD关于点D成中心对称的三角形
(2)A′B=AC　　(3)AB+AC＞2AD　　理由:因为△ACD与△A′BD关于点D成中心对称，所以AD=A′D,AC=A′B.在△ABA′中，根据两点之间，线段最短，得AB+A′B＞AA′，所以AB+AC＞AD+A′D,即AB+AC＞2AD.
　　　　　　　　　