1. 在$\triangle ABC$和$\triangle DEF$中,若$AB = 7$,$BC = 6$,$AC = 5$,$ED = \dfrac{7}{2}$,$EF = \dfrac{5}{2}$,$DF = 3$,则下列结论正确的是(
B
)
A.$\angle A = \angle D$
B.$\angle A = \angle E$
C.$\angle A = \angle F$
D.$\angle C = \angle D$
答案:1.B
解析:
在$\triangle ABC$中,$AB = 7$,$BC = 6$,$AC = 5$;在$\triangle DEF$中,$ED = \dfrac{7}{2}$,$EF = \dfrac{5}{2}$,$DF = 3$。
计算对应边的比值:
$\dfrac{AB}{ED} = \dfrac{7}{\dfrac{7}{2}} = 2$,
$\dfrac{AC}{EF} = \dfrac{5}{\dfrac{5}{2}} = 2$,
$\dfrac{BC}{DF} = \dfrac{6}{3} = 2$。
所以$\dfrac{AB}{ED} = \dfrac{AC}{EF} = \dfrac{BC}{DF} = 2$,故$\triangle ABC ∼ \triangle EDF$(三边成比例的两个三角形相似)。
相似三角形对应角相等,所以$\angle A = \angle E$。
B
2. 如图,$\triangle ABC$和$\triangle DEF$是正方形网格中的两个格点三角形,则$\angle BAC$的度数为(
D
)

A.$105^{\circ}$
B.$115^{\circ}$
C.$125^{\circ}$
D.$135^{\circ}$
答案:2.D 解析:设每个小正方形的边长为1,则$AC=\sqrt{10}$,$AB=\sqrt{5}$,$BC=5$,$EF=2$,$ED=\sqrt{2}$,$DF=\sqrt{10}$,所以$\frac{AC}{EF}=\frac{AB}{ED}=\frac{BC}{DF}=\frac{\sqrt{10}}{2}$,所以$\triangle ABC∼\triangle EDF$,所以$\angle BAC=\angle DEF$。又$\angle DEF=90^{\circ}+45^{\circ}=135^{\circ}$,所以$\angle BAC=135^{\circ}$。
3. 已知$AB = 4$,$BC = 5$,$AC = 8$,$DE = \dfrac{5}{3}$,$DF = \dfrac{10}{3}$,则当$EF =$
$\frac{25}{12}$
时,$\triangle ABC \backsim \triangle DEF$.
答案:3.$\frac{25}{12}$
4. 新素养 几
何直观(教材 P61 练习 3 变式)如图,已知$\dfrac{AB}{AD} = \dfrac{BC}{DE} = \dfrac{AC}{AE}$,$\angle BAD = 20^{\circ}$,$\angle DAE = 60^{\circ}$,则$\angle DAC$的度数为
$40^{\circ}$
.
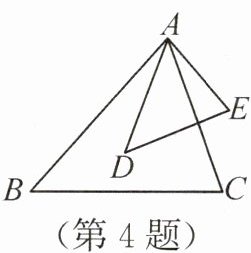
答案:4.$40^{\circ}$解析:因为$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,所以$\triangle ABC∼\triangle ADE$,所以$\angle BAC=\angle DAE=60^{\circ}$。因为$\angle BAD=20^{\circ}$,所以$\angle DAC=\angle BAC - \angle BAD = 40^{\circ}$。
5. 新素养
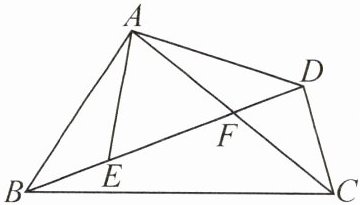
推理能力 如图,在四边形$ABCD$中,$AC$,$BD$相交于点$F$,点$E$在$BD$上,且$\dfrac{AB}{AE} = \dfrac{BC}{ED} = \dfrac{AC}{AD}$.
(1)试问:$\angle BAE$与$\angle CAD$相等吗?为什么?
(2)试判断:$\triangle ABE$与$\triangle ACD$是否相似?并说明理由.
]
答案:5.(1)$\angle BAE$与$\angle CAD$相等。理由如下:因为$\frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,所以$\triangle ABC∼\triangle AED$,所以$\angle BAC=\angle EAD$,所以$\angle BAC - \angle EAF=\angle EAD - \angle EAF$,即$\angle BAE=\angle CAD$。
(2)$\triangle ABE$与$\triangle ACD$相似。理由如下:因为$\frac{AB}{AE}=\frac{AC}{AD}$,所以$\frac{AB}{AC}=\frac{AE}{AD}$。又$\angle BAE=\angle CAD$,所以$\triangle ABE∼\triangle ACD$。
6. (2025·江苏南京模拟)若$\triangle ABC$的每条边长增加各自的$10\%$得$\triangle A'B'C'$,则$\angle B'$的度数与其对应角$\angle B$的度数相比,(
D
)
A.增加了$10\%$
B.减少了$10\%$
C.增加了$(1 + 10\%)$
D.没有改变
答案:6.D
解析:
因为三角形的每条边长增加各自的10%,所以新三角形与原三角形的对应边之比为$(1 + 10\%) : 1 = 1.1:1$,即对应边成比例。根据相似三角形的判定定理,三边对应成比例的两个三角形相似,所以$\triangle A'B'C' ∼ \triangle ABC$。又因为相似三角形的对应角相等,所以$\angle B' = \angle B$,即$\angle B'$的度数与其对应角$\angle B$的度数相比没有改变。
D
7. 新素养
应用意识 在如图所示的象棋盘(每个小正方形的边长均相等)中,根据“马走日”的规则,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似的“马”的落点位置是(
B
)
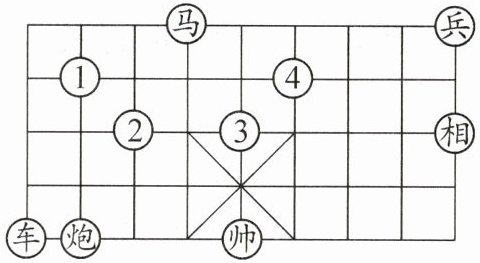
A.①处
B.②处
C.③处
D.④处
答案:7.B
8. 一个三角形木架三条边的长分别是$75\mathrm{cm}$,$100\mathrm{cm}$,$120\mathrm{cm}$,要做一个与它相似的三角形木架,现有长为$60\mathrm{cm}$和$120\mathrm{cm}$的两根木条,要求以其中一根为一边,从另一根上截下两段作为另外两边(允许有余料),则不同的截法有(
B
)
A.$1$种
B.$2$种
C.$3$种
D.$4$种
答案:8.B 解析:①当以$120\mathrm{cm}$长的木条为一边时,另两边长的和应大于$120\mathrm{cm}$,不合题意;②当以$60\mathrm{cm}$长的木条为一边时,设另外两边的长分别为$x\mathrm{cm}$和$y\mathrm{cm}(x<y)$。由题意,得$\frac{60}{75}=\frac{x}{100}=\frac{y}{120}$或$\frac{60}{100}=\frac{x}{75}=\frac{y}{120}$或$\frac{60}{120}=\frac{x}{75}=\frac{y}{100}$,解得$x = 80$,$y = 96$或$x = 45$,$y = 72$或$x = 37.5$,$y = 50$。因为$80 + 96 = 176>120$,$45 + 72 = 117<120$,$37.5 + 50 = 87.5<120$,所以满足题意的不同的截法有2种。
易错警示
注意分类讨论,避免漏解。
9. 在$\triangle ABC$中,已知$AB = 4$,$BC = 5$,$CA = 6$.
(1)如果$DE = 10$,那么当$EF =$
$12.5$
,$FD =$
$15$
时,$\triangle DEF \backsim \triangle ABC$;
(2)如果$DE = 10$,那么当$EF =$
$12$
,$FD =$
$8$
时,$\triangle FDE \backsim \triangle ABC$.
答案:9.(1)$12.5$ $15$ (2)$12$ $8$