跟踪练习3 新素养
应用意识 如图,工地上有一根圆柱形水泥管被截去了一部分,它现在的体积是(
494.55
)立方分米。
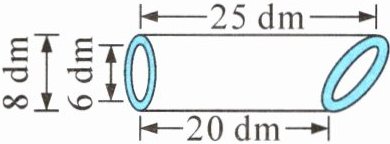
答案:[跟踪练习3] $494.55$
解析:
$8÷2=4(\mathrm{dm})$
$6÷2=3(\mathrm{dm})$
$3.14×(4^2-3^2)×(20+25)÷2$
$=3.14×(16-9)×45÷2$
$=3.14×7×45÷2$
$=3.14×315÷2$
$=989.1÷2$
$=494.55(\mathrm{dm}^3)$
494.55
类型 稍复杂的物体入水问题
例 一个内底面积是 $15 \mathrm{ cm}^2$ 的圆柱形玻璃杯中装有 $3 \mathrm{ cm}$ 深的水。现把一个底面半径是 $1 \mathrm{ cm}$、高是 $5 \mathrm{ cm}$ 的圆柱形铁块垂直放入玻璃杯中(水没有溢出),水面上升了多少厘米?($\pi$ 取 $3$)
答案:这道题没有说明圆柱形铁块是否浸没在水中,所以要先判断高是 $5 \mathrm{ cm}$ 的圆柱形铁块垂直放入水深 $3 \mathrm{ cm}$ 的玻璃杯后是全部浸在水中,还是部分浸在水中。因为全部浸在水中的情况比较好解决,所以可以先假设圆柱形铁块全部浸在水中,此时原有水的体积与圆柱形铁块的体积之和为 $15 × 3 + 3 × 1^2 × 5 = 60 (\mathrm{cm}^3)$,水面高 $60 ÷ 15 = 4 (\mathrm{cm})$,因为圆柱形铁块的高是 $5 \mathrm{ cm}$,$4 < 5$,所以圆柱形铁块不可能全部浸在水中。
现在来考虑圆柱形铁块没有全部浸在水中时,水面上升的高度。把圆柱形铁块垂直放入玻璃杯中,水所覆盖的底面积是玻璃杯的内底面积与圆柱形铁块的底面积之差,即 $15 - 3 × 1^2 = 12 (\mathrm{cm}^2)$。而水的体积是不变的,即 $15 × 3 = 45 (\mathrm{cm}^3)$。这时只要考虑水的体积,此时水的形状如图,水的底面是一个环形,这个空心圆柱的体积就是水的体积,用水的体积除以水的底面积就可以求出圆柱形铁块放入水中后,水面的高度是 $45 ÷ 12 = 3.75 (\mathrm{cm})$,所以水面上升了 $3.75 - 3 = 0.75 (\mathrm{cm})$。
规范解答
假设圆柱形铁块完全浸在水中。$15 × 3 = 45 (\mathrm{cm}^3)$ $45 + 3 × 1^2 × 5 = 60 (\mathrm{cm}^3)$ $60 ÷ 15 = 4 (\mathrm{cm})$ 因为 $4 < 5$,所以圆柱形铁块不可能全部浸在水中。
$15 - 3 × 1^2 = 12 (\mathrm{cm}^2)$ $45 ÷ 12 = 3.75 (\mathrm{cm})$ $3.75 - 3 = 0.75 (\mathrm{cm})$
答:水面上升了 $0.75$ 厘米。
跟踪练习
一个盛有水的圆柱形容器,内底面半径为 $5 \mathrm{ cm}$,容器深 $20 \mathrm{ cm}$,水深 $15 \mathrm{ cm}$。现在将一个底面半径是 $2 \mathrm{ cm}$、高是 $17 \mathrm{ cm}$ 的圆柱形铁块垂直放入容器内,这时容器内水深(
17.72
)厘米。
答案:思维创新探究
[跟踪练习] 17.72 解析 假设圆柱形铁块完全浸在水中,此时原有水的体积与圆柱形铁块的体积之和为$ 3.14 × 5^{2} × 15 + 3.14 × 2^{2} × 17 = 1391.02(cm^{3}),$水面高$ 1391.02 ÷ (3.14 × 5^{2}) = 17.72(cm),$17.72 > 17,所以圆柱形铁块全部浸在水中,这时容器内水深 17.72 厘米。