跟踪练习 2
在一个圆柱形的储水桶里,把一根底面直径是 8 厘米的铜棒全部放入水中,这时水面上升 10 厘米;把这根铜棒竖直拉出水面 6 厘米,水面下降 3 厘米。这根铜棒的体积是(
1004.8
)立方厘米。
答案:1004.8
解析:
设圆柱形储水桶的底面积为$S$平方厘米。
铜棒底面半径:$8÷2 = 4$厘米,铜棒底面积:$\pi×4^{2}=16\pi$平方厘米。
铜棒全部放入水中,水面上升10厘米,铜棒体积$V = 10S$。
拉出水面6厘米,下降水的体积等于6厘米铜棒体积:$3S=16\pi×6$,解得$S = 32\pi$。
铜棒体积$V=10S=10×32\pi = 320\pi$,$\pi$取3.14,$320×3.14 = 1004.8$立方厘米。
1004.8
例 3(教材 P23)
一个圆锥和一个圆柱底面积相等,体积的比是 $1:6$。如果圆锥的高是 4.2 厘米,圆柱的高是多少厘米?如果圆柱的高是 4.2 厘米,圆锥的高是多少厘米?
答案:第一问要求圆柱的高,因为不知道圆柱的体积和底面积,所以可用假设法来探究圆柱的高和圆锥的高之间的关系。假设圆柱的底面积和圆锥的底面积都是 $S$,圆柱的体积为 $V_{柱}$,圆柱的高为 $h_{柱}$,圆锥的体积为 $V_{锥}$,圆锥的高为 $h_{锥}$,那么体积计算公式 $V_{柱}=Sh_{柱}$,$V_{锥}=\frac{1}{3}Sh_{锥}$,可以得到 $\frac{1}{3}Sh_{锥}×6 = Sh_{柱}$,所以 $h_{锥}×2 = h_{柱}$,因此圆柱的高是圆锥的高的 2 倍。
规范解答
$4.2×2 = 8.4$(厘米) $4.2÷2 = 2.1$(厘米) 答:如果圆锥的高是 4.2 厘米,圆柱的高是 8.4 厘米。如果圆柱的高是 4.2 厘米,圆锥的高是 2.1 厘米。
跟踪练习 3(2025·合肥庐江县期末)
一个圆柱和一个圆锥的体积之比为 $2:1$,底面积之比为 $1:3$,则圆柱和圆锥的高的比是(
C
)。
A.$3:1$
B.$1:3$
C.$2:1$
答案:C
解析:
设圆柱的体积为$V_1$,底面积为$S_1$,高为$h_1$;圆锥的体积为$V_2$,底面积为$S_2$,高为$h_2$。
已知$\frac{V_1}{V_2}=\frac{2}{1}$,$\frac{S_1}{S_2}=\frac{1}{3}$。
圆柱体积公式:$V_1 = S_1h_1$,圆锥体积公式:$V_2=\frac{1}{3}S_2h_2$。
则$\frac{V_1}{V_2}=\frac{S_1h_1}{\frac{1}{3}S_2h_2}=\frac{3S_1h_1}{S_2h_2}$。
将$\frac{V_1}{V_2}=\frac{2}{1}$,$\frac{S_1}{S_2}=\frac{1}{3}$代入上式:
$\frac{2}{1}=\frac{3×\frac{1}{3}h_1}{h_2}=\frac{h_1}{h_2}$,即$\frac{h_1}{h_2}=\frac{2}{1}$。
C
例1 如图,用一块长方形铁皮做一个圆柱形铁皮水桶,求这个水桶的表面积和体积。
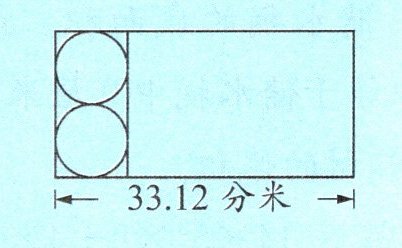
答案:规范解答 33.12÷(1+3.14)=8(分米)
8×2=16(分米) 表面积:$3.14×8×16+3.14×(8÷2)^2×2=502.4($平方分米)
体积:$3.14×(8÷2)^2×16=803.84($立方分米)
答:这个水桶的表面积是502.4平方分米,体积是803.84立方分米。