4. 新情境
知识科普 印刷用纸通常用 A2、A3、A4、A5 等编号表示大小规格,A4 纸是 A3 纸的一半,A5 纸是 A4 纸的一半。按照这样的编号规则,A5 的面积是 A2 纸的(
12.5
)%。
答案:4. 12.5
解析:
设A2纸的面积为$S$。
因为A3纸是A2纸的一半,所以A3纸面积为$\frac{1}{2}S$;
A4纸是A3纸的一半,所以A4纸面积为$\frac{1}{2}×\frac{1}{2}S = \frac{1}{4}S$;
A5纸是A4纸的一半,所以A5纸面积为$\frac{1}{2}×\frac{1}{4}S=\frac{1}{8}S$。
A5纸面积是A2纸面积的$\frac{\frac{1}{8}S}{S}×100\% = 12.5\%$。
12.5
5. 如图,如果点 C 表示的数是$\frac{2}{5}$,那么点 B 表示的数是(
$\frac{1}{5}$
);如果点 D 表示的数是 100,那么点 A 表示的数是(
-20
)。
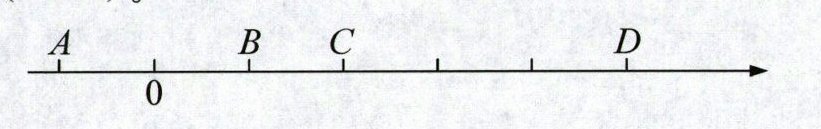
答案:5. $\frac{1}{5}$ -20
6. 把一根 5 米长的铁丝剪成同样长的 7 段,第 3 段长(
$\frac{5}{7}$
)米,每段长度是 1 米的$\frac{( )}{( )}$
答案:6. $\frac{5}{7}$ $\frac{5}{7}$
7. 一个数的最小倍数是 24,把这个数分解质因数(
24=2×2×2×3
);一个数的因数一共有 7 个,按从小到大的顺序排列,第 4 个因数是 8,这个数是(
64
)。
答案:7. 24=2×2×2×3 64
8. 鞋的尺码是指鞋内底的长度,通常用“码”或“厘米”作单位,它们之间的关系可以用 y=2x-10 来表示(y 表示码数,x 表示厘米数)。丽丽买了一双内底长度是 23 厘米的鞋,她买的是(
36
)码的鞋;爸爸买了一双 41 码的鞋,他的鞋内底长(
25.5
)厘米。
答案:8. 36 25.5
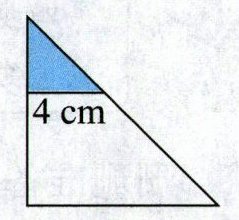
9. 亮点原创 如图,一个等腰直角三角形剪掉一个三角形后,还剩下一个梯形。已知梯形的面积是 42 平方厘米,上底是 4 厘米,梯形的高是(
6
)厘米。
答案:9. 6
解析:
设梯形的高是$h$厘米,下底为$b$厘米。
因为原图形是等腰直角三角形,剪掉一个三角形后剩下梯形,所以原等腰直角三角形的直角边为$b$,剪掉的小等腰直角三角形的直角边为$4$厘米,且梯形的高$h = b - 4$,即$b = h + 4$。
梯形面积公式:$\frac{(上底 + 下底)×高}{2}$,已知面积$42$平方厘米,上底$4$厘米,可得:
$\frac{(4 + b)h}{2} = 42$
将$b = h + 4$代入上式:
$\frac{(4 + h + 4)h}{2} = 42$
$\frac{(h + 8)h}{2} = 42$
$h(h + 8) = 84$
$h^2 + 8h - 84 = 0$
解方程:$(h + 14)(h - 6) = 0$,解得$h = 6$($h = -14$舍去)。
6
10. 新趋势 评
价说明 在一次投篮活动中,10 名同学共投进 61 个球。小华说:“总有一名同学至少投进 7 个球。”你认为小华说得对吗?(
对
)(填“对”或“不对”)
请说明你的理由:
61÷10=6(个)⋯⋯1(个) 6+1=7(个)
。
答案:10. 对 61÷10=6(个)⋯⋯1(个) 6+1=7(个)(理由合理即可)
解析:
对
$61÷10 = 6$(个)$······1$(个)
$6 + 1=7$(个)
11. 明明沿着直尺的方向将橡皮筋拉直(如下图)。如果点 A 的位置固定不变,沿原来的方向将橡皮筋拉长,使点 C 的位置在 15 厘米处,那么此时点 B 的位置在(
10
)厘米处。

答案:11. 10
12. 在 2000 多年前,古埃及人总喜欢把分数转化成分子是 1 的分数来计算,所以后人常把分子是 1 的分数称为埃及分数。埃及分数在计算中有着重要的规律:$\frac{1}{n×(n+1)}=\frac{1}{n}-\frac{1}{n+1}$(n 是非 0 自然数)。例如,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$。请根据这个规律计算:$\frac{2}{3×4}+\frac{2}{4×5}+\frac{2}{5×6}+\frac{2}{6×7}+···+\frac{2}{2023×2024}+\frac{2}{2024×2025}=$(
$\frac{1348}{2025}$
)。
答案:12. $\frac{1348}{2025}$
解析:
$\begin{aligned}&\frac{2}{3×4}+\frac{2}{4×5}+\frac{2}{5×6}+···+\frac{2}{2024×2025}\\=&2×(\frac{1}{3×4}+\frac{1}{4×5}+\frac{1}{5×6}+···+\frac{1}{2024×2025})\\=&2×[(\frac{1}{3}-\frac{1}{4})+(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})+···+(\frac{1}{2024}-\frac{1}{2025})]\\=&2×(\frac{1}{3}-\frac{1}{2025})\\=&2×(\frac{675}{2025}-\frac{1}{2025})\\=&2×\frac{674}{2025}\\=&\frac{1348}{2025}\end{aligned}$
13. (2025·南京江宁区期末)如图,用“十字形”分割正方形,分割一次,分割成 4 个正方形;分割两次,分割成 7 个正方形(不计组合成的正方形);分割三次,分割成 10 个正方形。如果连续用“十字形”分割 5 次,分割成(
16
)个正方形;若连续分割 n 次,则会分割成(
1+3n
)个正方形。

答案:13. 16 1+3n 解析:观察题图中正方形的个数,可发现以下规律:分割1次,正方形个数为1+3×1;分割2次,正方形个数为1+3×2;分割3次,正方形个数为1+3×3……分割n次,正方形个数为(1+3n)个。