6. 学校劳动社团制作了一个水箱,相关数据如下图①,打开水龙头,给这个水箱注水,注水时间和水位高度的关系如下图②,其中B点的水位高度是A点水位高度的2倍。
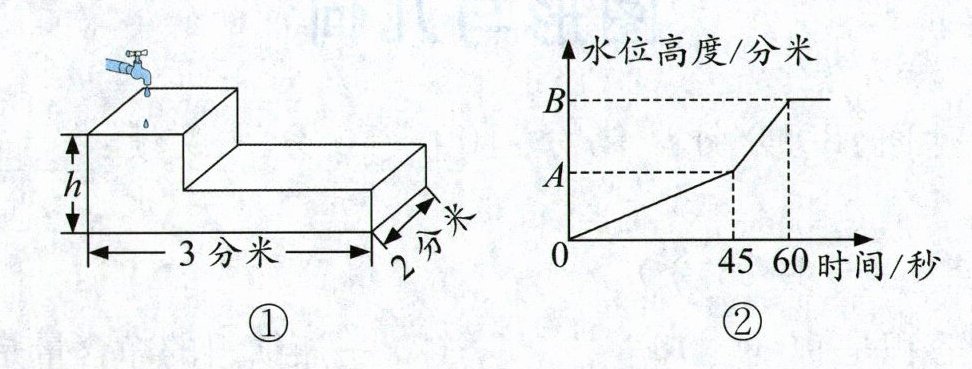
(1)由图可知,(
60
)秒后水箱注满了水,此时应该关闭水龙头。(2分)
(2)以0.1升/秒的速度往水箱里注水,可求得这个水箱的容积是(
6
)升。通过计算求出这个水箱的高度h。(5分)
答案:6.(1)60 (2)6 0.1×45=4.5(升) 4.5升=4.5立方分米 4.5÷(3×2)×2=1.5(分米)
1. 如图,在四边形ABCD中,AB=3BE,AD=3AF,平行四边形BODC的面积是48平方厘米,四边形AEOF的面积是(
24
)平方厘米。(4分)
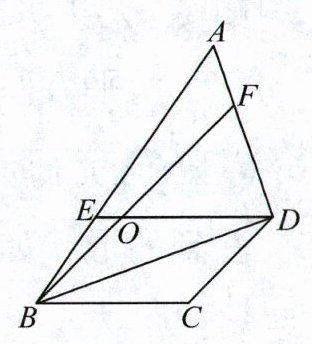
答案:1.24 解析 从题图中可以看出,三角形ABF与三角形ABD的高相等,AD=3AF,则三角形ABD的面积是三角形ABF面积的3倍;同理可得,三角形ABD的面积是三角形BDE面积的3倍。由此可以推出,三角形ABF的面积等于三角形BDE的面积。若从这两个三角形中同时减去三角形BOE,则剩下的图形面积相等,即四边形AEOF与三角形BOD的面积相等。因为三角形BOD的面积是平行四边形BODC面积的一半,所以四边形AEOF的面积也是平行四边形BODC面积的一半。四边形AEOF的面积为48÷2=24(平方厘米)。
解析:
证明:
∵AD=3AF,△ABF与△ABD高相等,
∴S△ABD=3S△ABF。
∵AB=3BE,△BDE与△ABD高相等,
∴S△ABD=3S△BDE。
∴S△ABF=S△BDE。
∵S△ABF=S四边形AEOF+S△BOE,
S△BDE=S△BOD+S△BOE,
∴S四边形AEOF=S△BOD。
∵四边形BODC是平行四边形,
∴S△BOD=$\frac{1}{2}$S平行四边形BODC=$\frac{1}{2}$×48=24(平方厘米)。
∴S四边形AEOF=24平方厘米。
24
2. 一个底面半径为2分米、高为4分米的圆柱形容器里装有部分水。当容器底面的一点紧贴着桌面倾斜时(如图,单位:分米),容器里的水刚好不溢出。容器里的水有多少升? (容器壁的厚度忽略不计)(6分)
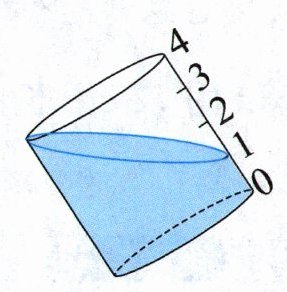
答案:$2.3.14×2^2 ×4=50.24($立方分米$) 3.14×2^2 ×(4-1)÷2=18.84($立方分米) 50.24-18.84=31.4(立方分米) 31.4立方分米=31.4升 解析 先根据圆柱的体积计算公式求出容器的容积是$3.14×2^2 ×4=50.24($立方分米);无水的部分看作是一个底面半径为2分米、高为(4-1)分米的圆柱的一半,再根据圆柱的体积计算公式求出无水部分的体积是$3.14×2^2 ×(4-1)÷2=18.84($立方分米);最后,用容器的容积减去无水部分的体积即可求解。
解析:
$3.14×2^{2}×4=50.24$(立方分米)
$3.14×2^{2}×(4-1)÷2=18.84$(立方分米)
$50.24-18.84=31.4$(立方分米)
$31.4$立方分米$=31.4$升