3. (2025·南通海安市期末)如右图,用4根木条围成一个长方形框架,将它拉成平行四边形,在这个变化过程中,平行四边形的面积和高(
B
)。
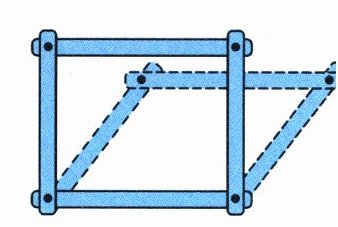
A.不成比例
B.成正比例
C.成反比例
D.不相关联
答案:3. B
4. 下面关于正、反比例的说法中,正确的有(
A
)个。
① 如果甲、乙是两个成反比例的量,那么当甲增加50%时,乙一定会减少50%。
② 因为爸爸的年龄÷小华的年龄=3,所以爸爸的年龄与小华的年龄成正比例。
③ 因为$3x - 2y = 0$,所以$x$与$y$是不成比例的两个量。($x$、$y$都不为0)
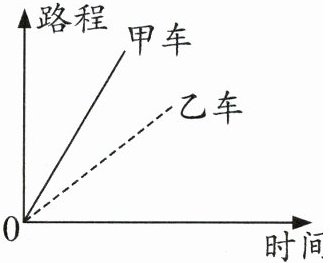
④ 右图是甲、乙两车所行时间与路程的关系图,从图中可以看出甲、乙两车所行路程与时间成正比例。
A.1
B.2
C.3
D.4
答案:4. A
解析:
①设甲、乙乘积为$k$($k\neq0$),甲增加$50\%$后为$1.5$甲,此时乙为$\frac{k}{1.5\mathrm{甲}}=\frac{2}{3}\mathrm{乙}$,减少$\frac{1}{3}\approx33.3\%\neq50\%$,错误。
②爸爸与小华年龄差固定,比值$3$随年龄增长变化,不成正比例,错误。
③由$3x - 2y = 0$得$\frac{x}{y}=\frac{2}{3}$(定值),$x$与$y$成正比例,错误。
④图中甲、乙均为过原点直线,路程与时间比值(速度)一定,成正比例,正确。
正确的有1个。A
5. (2025·苏州吴江区期末)轿车和货车同时从$A$、$B$两地出发。相向而行,相遇时轿车行了全程的$\dfrac{7}{13}$,那么轿车与货车的速度比是(
C
)。
A.$7:13$
B.$6:13$
C.$7:6$
D.$6:7$
答案:5. C
解析:
轿车与货车行驶时间相同,速度比等于路程比。相遇时轿车行了全程的$\dfrac{7}{13}$,则货车行了全程的$1 - \dfrac{7}{13} = \dfrac{6}{13}$,所以轿车与货车的速度比是$\dfrac{7}{13}:\dfrac{6}{13} = 7:6$。
C
6. 新情境
数学文化 我国古代数学名著《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送来谷米1534石,验得其中夹有谷粒,现从中抽取谷米一把,共数得254粒,其中夹有谷粒28粒,则这批谷米内夹有谷粒约(
B
)石。
A.134
B.169
C.268
D.338
答案:6. B
解析:
抽取的谷米中谷粒所占比例为$\frac{28}{254}$,这批谷米约有谷粒$1534×\frac{28}{254}\approx169$石。
B
1. 直接写出得数。(4分)
$475 - 298 =$
$0.8÷10\% =$
$2.6×\dfrac{5}{13} =$
$\dfrac{2}{3}×4÷\dfrac{2}{3}×4 =$
$1 - 0.09 =$
$\dfrac{6}{5}÷\dfrac{5}{6} =$
$\dfrac{2}{3} + \dfrac{1}{5} =$
$0.125×9×8 =$
答案:1. 177 8 1 16 0.91 $\frac{36}{25}$ $\frac{13}{15}$ 9
2. 计算下面各题,能简算的要简算。(6分)
$64×\dfrac{1}{4} + 4.36×25\%$
$\dfrac{2}{5}÷[ ( \dfrac{1}{2} + \dfrac{1}{20} )÷6 ]$
$15×( \dfrac{1}{5} + \dfrac{1}{7} )×14$
答案:2. 17.09 $\frac{48}{11}$ 72
解析:
$64×\frac{1}{4}+4.36×25\%$
$=64×0.25 + 4.36×0.25$
$=(64 + 4.36)×0.25$
$=68.36×0.25$
$=17.09$
$\frac{2}{5}÷[(\frac{1}{2}+\frac{1}{20})÷6]$
$=\frac{2}{5}÷[(\frac{10}{20}+\frac{1}{20})÷6]$
$=\frac{2}{5}÷[\frac{11}{20}÷6]$
$=\frac{2}{5}÷(\frac{11}{20}×\frac{1}{6})$
$=\frac{2}{5}÷\frac{11}{120}$
$=\frac{2}{5}×\frac{120}{11}$
$=\frac{48}{11}$
$15×(\frac{1}{5}+\frac{1}{7})×14$
$=15×14×(\frac{1}{5}+\frac{1}{7})$
$=15×14×\frac{1}{5}+15×14×\frac{1}{7}$
$=3×14 + 15×2$
$=42 + 30$
$=72$