1. 填一填。
(1) 在1,3,16,45,29,40,51中,(
16,40
)有因数2,奇数有(
1,3,45,29,51
),质数有(
3,29
),(
1
)既不是质数也不是合数。
(2) 628$□$既含有因数2,又是3的倍数。$□$里可以填(
2 或8
)。
(3) 已知$A=2×3×3×5×5,B=2×2×3×3×5$,A与B的最大公因数是(
90
),最小公倍数是(
900
)。
(4) (2025·淮安市期末)端午节红星社区给辖区内的清洁工人发放小礼包,社区准备了96个粽子、120个鸭蛋,打包成若干份(无剩余),要求每份粽子的个数相同,鸭蛋的个数也相同。红星社区最多能发给(
24
)位清洁工人。
答案:1.(1)16,40 1,3,45,29,51 3,29 1 (2)2 或8 (3)90 900 (4)24
2. 选一选。
(1) 如果a是一个质数,b是一个合数,且$a>b$,那么下面算式中,(
C
)的结果肯定是合数。
A. $a+b$
B. $a-b$
C. $a×b$
D. $a÷b$
(2) 如果m是奇数,n是偶数,下面结果是奇数的算式是(
A
)。
A. $m+n$
B. $2m+n$
C. $2m+2n$
D. $2mn$
答案:2.(1)C (2)A
3. 新情境 数学文化 古希腊数学家认为,如果一个数恰好等于它所有的因数(本身除外)相加的和,那么这个数是“完全数”。下面是“完全数”的是(
C
)。
A.16
B.20
C.28
D.36
答案:3.C
解析:
A.16的因数(本身除外):1、2、4、8,1+2+4+8=15≠16
B.20的因数(本身除外):1、2、4、5、10,1+2+4+5+10=22≠20
C.28的因数(本身除外):1、2、4、7、14,1+2+4+7+14=28
D.36的因数(本身除外):1、2、3、4、6、9、12、18,1+2+3+4+6+9+12+18=55≠36
C
4. 若A、B、C都为质数,且$A+B+C=20$,B和C的差为偶数,则$A=$(
2
)。
答案:4.2
解析:
因为B和C的差为偶数,所以B和C同为奇数或同为偶数。质数中只有2是偶数,若B和C同为偶数,则B=C=2,此时A=20-2-2=16,16不是质数,不符合题意。所以B和C同为奇数,奇数+奇数=偶数,20是偶数,偶数-偶数=偶数,所以A为偶数,又因为A是质数,所以A=2。
5. 把一个长40厘米、宽32厘米、高28厘米的长方体木块锯成若干个大小相同的正方体木块,锯完后没有余料,最少可以锯成多少个正方体?
答案:5.(40,32,28)=4 40÷4=10(个) 32÷4=8 (个) 28÷4=7(个) 10×8×7=560(个)
6. 两个数的最大公因数是6,最小公倍数是36,则符合条件的数有(
2
)组。
答案:6.2 解析:6=2×3,36=2×3×2×3,这两个数是6和36,或者是2×3×2=12和2×3×3 =18。
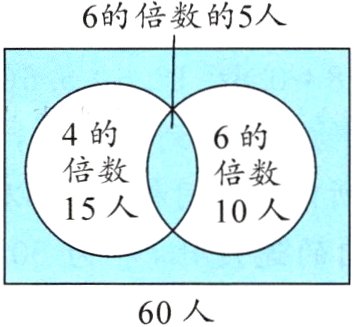
7. 亮点原创 60名同学面向老师站成一排,从左往右依次报数:1,2,3,…,60。报完后,老师让所报的数是4的倍数的同学向后转,接着让所报的数是6的倍数的同学向后转,现在仍面向老师的同学有多少人?
答案:7.60−[(15−5)+(10−5)]=45(人) 现在仍面向老师的同学有45人。解析:如图,面向老师的人数即图中涂色部分的人数。
既是4的倍数又是6的倍数的5人
4的倍数15人
6的倍数10人
60人