1. 判断下面每题中的两种量是否成反比例关系,成反比例的画“√”,不成反比例的画“×”。
(1)电脑 D 盘的总空间一定,已使用的空间和剩余的空间。(
×
)
(2)苹果的单价一定,购买苹果的总价和数量。(
×
)
(3)生产电视机的总台数一定,每天生产的台数和所用的天数。(
√
)
(4)铺地面积一定,每块正方形方砖的边长与所需正方形方砖的块数。(
×
)
答案:1.(1) × (2) × (3) √ (4) ×
2. 选一选。
(1)(2025·盐城市期末)“盐小勺”毛绒玩具是盐城的地方文创作品。妈妈用 600 元购买不同款式的“盐小勺”毛绒玩具,购买的单价和数量如下表:
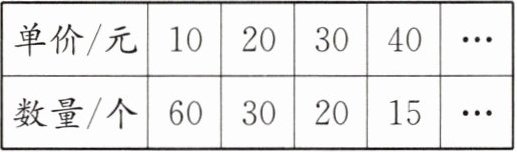
从表中可以看出,单价与数量(
B
)。
A. 成正比例
B. 成反比例
C. 不成比例
D. 不相关联
(2)下面两种量成反比例的是(
C
)。
A. 圆柱的底面积一定,圆柱的体积和高
B. 减数一定,被减数和差
C. 长方形的面积一定,长和宽
(3)一个非零自然数与它的倒数一定(
B
)。
A. 成正比例
B. 成反比例
C. 不成比例
答案:2.(1) B (2) C (3) B
3. 若$\frac{x}{5}=\frac{1}{2}:y$($x$、$y$均不为 0),则 $x$ 和 $y$ 成(
反
)比例。
答案:3. 反
4. 如图是自行车上的两个齿轮,通过链条转动。在同一时间内,大、小齿轮转过的齿数是相同的。
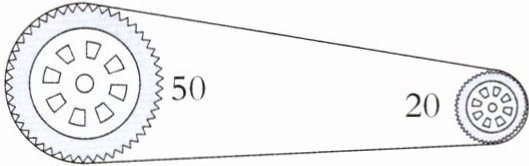
(1)转过的总齿数一定时,每个齿轮的齿数与转过的圈数成(
反
)比例。
(2)大齿轮有 50 个齿,小齿轮有 20 个齿。如果大齿轮每分钟转 12 圈,那么小齿轮每分钟转(
30
)圈。
答案:4.(1) 反 (2) 30
5. (亮点原创)三角形的底边长 $a$ 厘米,高 $h$ 厘米,$a$ 与 $h$ 的关系如图。
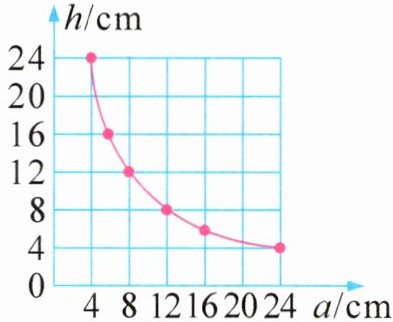
(1)三角形的面积是(
48
)平方厘米。
(2)当 $a = 16$ 时,$h =$(
6
)。
答案:5.(1) 48 解析 从图像中选一点,找出$a$和$h$相对应的一组数据,就可求出三角形的面积。
例如:$24 × 4 ÷ 2 = 48(\mathrm{cm}^2)$或$12 × 8 ÷ 2 = 48(\mathrm{cm}^2)$。(2) 6 解析 因为$a$和$h$的乘积一定,所以它们成反比例,$h = 48 × 2 ÷ 16 = 6$。
6. 一艘轮船所带的柴油最多可以用 6 小时,驶出时顺风,每小时航行 30 千米;驶回时逆风,每小时航行的路程是顺风时的$\frac{4}{5}$。这艘轮船最多驶出多远就应往回航行?
答案:6.$6 × \frac{4}{4+5} = \frac{8}{3}$(时) $30 × \frac{8}{3} = 80$(千米)
解析 轮船驶出与驶回的路程相等,则轮船驶出与驶回的速度和对应所用时间成反比例,由于轮船驶回的速度是驶出的$\frac{4}{5}$,则驶回的时间是驶出的$\frac{5}{4}$。把6小时按$5:4$进行分配,其中4份表示的量是驶出的时间,由此可求出驶出的路程。