3. 如图是一个上半部分为圆柱,下半部分为圆锥的可密封的容器。容器内现有水的高度为22厘米,圆柱和圆锥底面半径均为10厘米,高均为18厘米,把这个容器里的水倒过来,水面高多少米? 这时水与容器的接触面积是多少平方厘米? (π取3)
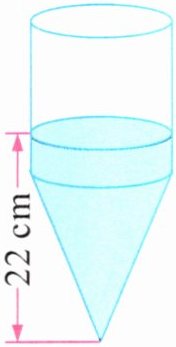
答案:3.$\frac{1}{3} × 3 × 10^{2} × 18+3 × 10^{2} × (22-18)=3000$(立方厘米)
水面高:$3000 ÷ (3 × 10^{2})=10$(厘米)
水与容器的接触面积:$3 × 10^{2}+3 × (10 × 2) × 10=900$(平方厘米)
4. 蜂窝煤是由无烟煤制成的。每个蜂窝煤有12个相同的空心小圆柱,如图①。

(1) 制作一个蜂窝煤需要用无烟煤多少立方厘米? 下面计算方法中,错误的是(
③
)。(填序号)
① 大圆柱的体积—12个小圆柱的体积
② 蜂窝煤的底面积×高
③ (大圆柱的底面周长—12个小圆柱的底面周长之和)×高
(2) 如图②,现有一个圆锥形煤堆,用这堆煤可以制作多少个蜂窝煤?
答案:4.(1)③ (2)$3.14 × (12 ÷ 2)^{2} × 10-3.14 × (2 ÷ 2)^{2} × 10 × 12=753.6$(立方厘米)
$3.14 × (4 ÷ 2)^{2} × 0.9 × \frac{1}{3}=3.768$(立方米)
3.768立方米$=3768000$立方厘米
$3768000 ÷ 753.6=5000$(个) 解析 根据题图①可求出一个蜂窝煤的体积是$3.14 × (12 ÷ 2)^{2} × 10-3.14 × (2 ÷ 2)^{2} × 10 × 12=753.6$(立方厘米)。根据题图②可求出圆锥形煤堆的体积为$3.14 × (4 ÷ 2)^{2} × 0.9 × \frac{1}{3}=3.768$(立方米),即3768000立方厘米。最后用煤堆的体积除以一个蜂窝煤的体积就可求出制作蜂窝煤的个数,即为$3768000 ÷ 753.6=5000$(个)。
5. 如图,亮亮准备用一张边长为24厘米的正方形卡纸做一个尽可能大的圆柱形笔筒。(π取3)

(1) 做成的圆柱形笔筒的体积是多少?
(2) 剩余边角料(涂色部分)的面积是多少?
答案:5.(1)当圆柱形笔筒的高为24厘米时,底面直径为$24 ÷ (1+3)=6$(厘米),体积为$3 × (6 ÷ 2)^{2} × 24=648$(立方厘米)。当圆柱形笔筒的底面周长为24厘米时,底面直径为$24 ÷ 3=8$(厘米),高为$24-8=16$(厘米),体积为$3 × (8 ÷ 2)^{2} × 16=768$(立方厘米)。 $648<768$ 做成的圆柱形笔筒的体积是768立方厘米。
(2)$24 × 8-3 × (8 ÷ 2)^{2}=144$(平方厘米)
6. 李师傅向下面左图形状的空容器(由上、下两个圆柱组成)中匀速注油,直至注满。注油过程中,容器中油的高度与所用时间的关系如下面右图。
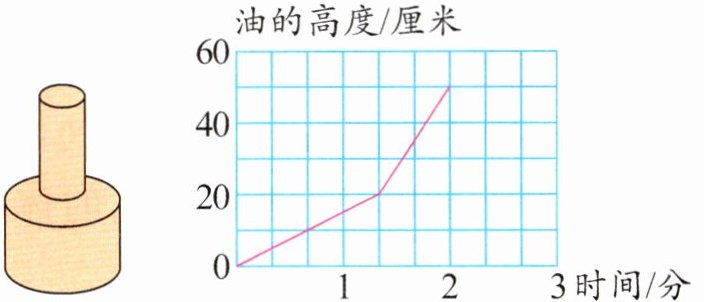
(1) 把容器下面的大圆柱注满需(
$\frac{4}{3}$
)分钟。
(2) 上面的小圆柱高(
30
)厘米。
(3) 如果下面的大圆柱底面积是48平方厘米,那么大圆柱的体积是多少立方厘米? 上面小圆柱的底面积是多少平方厘米?
答案:6.(1)$\frac{4}{3}$厘米 (2)30 (3)$48 × 20=960$(立方
$960 ÷ \frac{4}{3} × (2-\frac{4}{3})=480$(立方
米) $480 ÷ 30=16$(平方厘米) 解析 大圆柱的体积用底面积乘高求得是$48 × 20=960$(立方厘米)。要求小圆柱的体积,先求出每分钟注油的体积为$960 ÷ \frac{4}{3}=720$(立方厘米),根据注油时间求出小圆柱的体积为$720 × (2-\frac{4}{3})=480$(立方厘米),最后求出小圆柱的底面积是$480 ÷ 30=16$(平方厘米)。