7. 小明和小刚用如图的两个质地均匀的转盘做游戏,规则如下:同时转两个转盘,当所得两数之积为奇数时,小明得 1 分;当所得两数之积为偶数时,小刚得 1 分. 这个游戏对双方公平吗?若公平,说明理由;若不公平,如何修改规则才能使游戏对双方公平?

答案:解:∵P 奇$=\frac {1}{3},$P 偶$=\frac {2}{3}$
∴这个游戏对双方是不公平的
对规则可做不同的修改,如:将“为奇数”和“为偶数”
分别改为“大于2”和“不大于2”
8. 有 3 张扑克牌,分别是红桃 3、红桃 4 和黑桃 5. 把牌洗匀后甲先抽取 1 张,记下花色和数字后将牌放回,洗匀后乙再抽取 1 张.
(1) 列表或画树状图表示所有取牌的可能性.
(2) 甲、乙两人做游戏,现有两种方案. A 方案:若两次抽得相同花色则甲胜,否则乙胜. B 方案:若两次抽得的牌面数字和为奇数则甲胜,否则乙胜. 甲选择哪种方案获胜概率更高?
答案:解:(1)画树状图如下
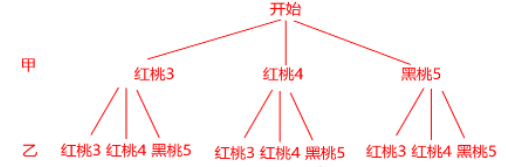
∴所有取牌的可能性共有9种
(2) 两次抽得相同花色的有5种情况
∴A方案:P(甲胜$)=\frac {5}{9}$
又∵两次抽得数字和为奇数的有4种情况
∴B方案:P(甲胜$)=\frac {4}{9} $
∴甲应选择A方案
9. 小红和小明在操场做游戏,他们先在地上分别画了半径为 2 m 和 3 m 的同心圆(如图①),蒙上眼睛在圈外向圈内掷小石子. 掷中阴影小红胜,否则小明胜(未掷入圈内或掷中两圆的边界线则重掷).
(1) 你认为游戏公平吗?为什么?
(2) 请你在图②中也画一个同心圆,再将部分涂成阴影,并作简要说明,使你设计的游戏方案对双方公平.

答案:解:(1)不公平;
∵P(阴$)=\frac {5}{9},$即小红胜率为$ \frac {5}{9},$小明胜率为$ \frac {4}{9}$
∴游戏对双方不公平
(2)方案不唯一
例如,设已有圆的半径为a,画半径$ \frac {\sqrt{2}}{2}\ \mathrm {a}$的同心圆,
再将圆环部分涂成阴影(其他游戏规则不变)
