17. 阅读下列内容:
为了求 $ \tan 15^{\circ} $ 的值,可构造如图所示的直角三角形:作 $ \mathrm{Rt}\triangle ABC $,使 $ \angle C = 90^{\circ} $,$ \angle ABC = 30^{\circ} $,延长 $ CB $ 到点 $ D $,使 $ BD = AB $,得 $ \angle D = 15^{\circ} $. 设 $ AC = k $,则 $ AB = BD = 2k $,$ BC = \sqrt{3}k $,所以 $ \tan 15^{\circ} = \tan D = \frac{AC}{CD} = \frac{k}{(2 + \sqrt{3})k} = \frac{1}{2 + \sqrt{3}} = 2 - \sqrt{3} $. 试求 $ \tan 22.5^{\circ} $ 的值(保留根号).

答案:解:作 Rt△ABC,使∠C=90°,∠ABC=45°
延长CB到点D,使得BD=AB,得∠D=22.5°
设AC=x,则$AB=BD=\sqrt 2x,$BC=AC=x
∴$tan 22.5°=tanD=\frac {AC}{CD}=\frac x{(1+\sqrt 2)x}=\sqrt 2-1$
18. 如图,$ \angle MON = 60^{\circ} $,点 $ P $ 在 $ \angle MON $ 内,点 $ P $ 到边 $ OM $ 的距离 $ PA = 3 \mathrm{ cm} $,点 $ P $ 到边 $ ON $ 的距离 $ PB = 12 \mathrm{ cm} $. 求 $ OP $ 的长(保留根号).

答案:解:延长BP交OM于点C
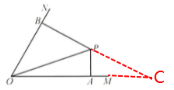
在Rt△PAC中,∵PA=3,∠C=30°
∴PC=2PA=6,$AC=\sqrt 3PA=3\sqrt 3$
∵PB=12
∴BC=18
在Rt△BCO中,∵∠PBO=90°,∠C=30°,BC=18
∴$OC=\frac {BC}{cos 30°}=12\sqrt 3$
∴$OA=OC-AC=9\sqrt 3$
∴$OP=\sqrt {OA^2+PA^2}=6\sqrt 7\ \mathrm {cm}$