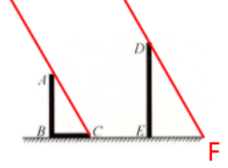
5. 如图,$ AB $ 和 $ DE $ 是地面上的两根立柱,$ AB = 5$ m,某一时刻 $ AB $ 在阳光下的投影 $ BC = 3$ m.
(1) 在图中画出此时 $ DE $ 在阳光下的投影;
(2) 设此时 $ DE $ 在阳光下的投影长为 $ a$ m,则 $ DE $ 的长为
$\frac{5a}{3}$
m.

答案:$\frac {5a}3$
6. 如图,为了测量路灯 $ S $ 的高度 $ h $,把一根长 $ 1.5$ m 的竹竿 $ AB $ 竖立在地面上,测得竹竿的影长 $ BC $ 为 $ 1$ m,然后拿着竹竿沿 $ OB $ 方向走了 $ 4$ m 到点 $ B' $,再把竹竿竖立在地面上(即 $ A'B' $),测得竹竿的影长 $ B'C' $ 为 $ 1.8$ m. 求路灯的高度.

答案:解:由题意得,AB//A'B'//OS
∵AB//OS
∴△ABC∽△SOC
∴$\frac {AB}{SO}=\frac {BC}{OC}$
∵A'B'//SO
∴△A'B'C'∽△SOC'
∴$\frac {A'B'}{SO}=\frac {B'C'}{OC'}$
∵AB=A'B'
∴$\frac {BC}{OC}=\frac {B'C'}{OC'}$
设OC=(x+1)m,OC'=(x+5.8)m
∴$\frac 1{x+1}=\frac {1.8}{x+5.8},$解得x=5
∴OB=5m,OC=6m
∵$\frac {AB}{SO}=\frac {BC}{OC}$
∴$\frac {1.5}h=\frac 16,$解得h=9
答:路灯的高度为9米。
7. 如图,某地冬至日中午,一温室的外墙 $ CD $ 高 $ 3$ m,其南面窗户的下沿与地面的距离 $ GC $ 为 $ 1$ m,且 $ CD $ 在地面上留下的影长 $ CF $ 为 $ 2$ m. 现欲在距点 $ C $ $ 7$ m 的正南方点 $ A $ 处建一幢 $ 12$ m 高的楼房 $ AB $(设点 $ A、C、F $ 在同一水平线上).
(1) 请按比例画出楼房 $ AB $ 及其在冬至日中午时的影长 $ AE $.
(2) 如上述楼房 $ AB $ 建成,冬至中午该温室外墙 $ CD $ 上窗户的光照是否会受到影响? 请说明理由.

答案:解:(1)如图所示
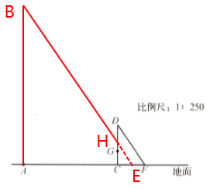
(2)会受到影响,理由如下:
令BE与CD的交点为点H
由平行投影可得,$\frac {CD}{CF}=\frac {AB}{AE}$
∵CD=3m,CF=2m,AB=12m
∴AE=8m
∵AC=7m
∴CE=1m
∵BE//DF
∴△CHE∽△CDF
∴$\frac {CH}{CE}=\frac {CD}{CF}=\frac 32$
∴$CH=\frac 32m$
∵CH>CG
∴窗户的光照会受到影响