5. 如图,A、B 两处被池塘隔开,为了测量 A、B 两处的距离,在 AB 外选一适当的点 C,连接 AC、BC,并分别取点 D、E,使 CD=$\frac{1}{3}$AC,CE=$\frac{1}{3}$BC,测得 DE=20 m,则 AB=
60
m.

答案:60
6. 如图,为了估算河的宽度,可以在河对岸选定一个目标作为点 A,在本岸选点 B 和 C,使 BC⊥AB,然后再选点 E,使 CE⊥BC,BC、AE 交于点 D. 如果此时测得 BD=120 m,DC=60 m,EC=50 m,求两岸间的距离 AB.

答案:解:∵BC⊥AB,CE⊥ BC
∴∠ABD=∠DCE=90°
∵∠ADB=∠CDE
∴△ABD∽△ECD
∴$\frac {AB}{EC}=\frac {BD}{DC}$
∵BD= 120m,DC=60m,EC= 50m
∴$\frac {AB}{50}=\frac {120}{60}$
∴AB= 100m
答:两岸间的距离AB为100m。
7. 如图,在一面与地面垂直的墙面的同侧有一根高 10 m 的旗杆 AB 和一根高度未知的电线杆 CD,它们都与地面垂直. 小丽进行如下测量:某一时刻,旗杆在墙面上的影长 EF 为 2 m,在地面上的影长 BF 为 10 m,电线杆在墙面上的影长 GH 为 3 m,在地面上的影长 DH 为 5 m. 求电线杆的高度.

答案:解:过点E作EM⊥AB,垂足为点M
过点G作GN⊥CD,垂足为点N,如图所示
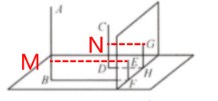
由平行投影可知,$\frac {AM}{ME}=\frac {CN}{NG}$
∵AB=10m,MB=EF=2m
∴AM=AB-MB=8m
∵ME=BF=10m,NG=DH=5m
∴$\frac 8{10}=\frac {CN}5$
∴CN=4m
∵GH=DN=3m
∴CD=CN+DN=7m
∴电线杆的高度为7米