1. 二次函数 $ y = 2(x - 3)^2 + 1 $ 图像的顶点坐标是
$(3,1)$
.
答案:(3,1)
2. 已知二次函数 $ y = 3x^2 + 4 $ 的图像经过点 $ A(-2,y_1) $、$ B(1,y_2) $、$ C(3,y_3) $,则 $ y_1 $、$ y_2 $、$ y_3 $ 的大小关系是
$y_3>y_1>y_2$
.
答案:$y_{3}\gt y_{1}\gt y_{2}$
3. 下列二次函数,图像不能由函数 $ y = 3x^2 $ 的图像平移得到的是(
D
).
A.$ y = 3x^2 + 2 $
B.$ y = 3(x - 1)^2 $
C.$ y = 3(x - 1)^2 + 2 $
D.$ y = x^2 + 3 $
答案:D
4. 在同一平面直角坐标系中,函数 $ y = mx + m $ 和 $ y = -mx^2 + 2x + 2 $($ m $ 是常数,且 $ m \neq 0 $)的图像可能是(
D
).

答案:D
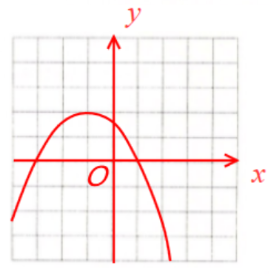
5. 已知二次函数图像的顶点是 $ (-1,2) $,且过点 $ \left(0,\dfrac{3}{2}\right) $.
(1)求该二次函数的表达式,并在图中画出它的图像.
(2)观察图像,直接写出当 $ y > 0 $ 时,$ x $ 的取值范围.
(3)求证:对任意实数 $ m $,点 $ M(m,-m^2) $ 都不在该二次函数的图像上.

答案:解:(1)设二次函数表达式为$y=a(x+1)^2+2$
将点(0,$\frac 32)$代入可得$\frac 32=a(0+1)^2+2$
∴$a=-\frac 12$
∴$y=-\frac 12(x+1)^2+2,$函数图像如图所示
(2)由图可得,-3<x<1
(3)若点M在此二次函数的图像上,
则$-\ \mathrm {m^2}=- \frac {1}{2} (m+1)^2+2$
化简,得$\ \mathrm {m^2}-2\ \mathrm {m}+3=0$
方程的判别式$b^2-4ac=4-12=-8\lt 0,$该方程无实数根
∴对任意实数m,点M(m,$-\ \mathrm {m^2})$都不在这个二次函数的图像上