9. 已知二次函数 $ y = mx^{2}+(m - 3)x - 1 $.
(1) 求证:不论 $ m $ 取何值,这个二次函数的图像都与 $ x $ 轴有两个公共点.
(2) 当 $ m = \frac{9}{2} $ 时,这个二次函数的图像与 $ x $ 轴交于 $ A $、$ B $ 两点,求线段 $ AB $ 的长.
(3) 设第(2)题中抛物线的顶点为 $ P $,求 $ \triangle ABP $ 的面积.
答案:证明:(1)∵判别式$b^2-4ac=(m-3)^2-4\ \mathrm {m}×(-1)=(m-1)^2+8\gt 0$
∴不论m 取何值,二次函数的图像都与x轴交于两点
(2) 当$m=\frac {9}{2} $时,$y=\frac 92x^2+\frac 32x-1$
令y=0,$\frac 92x^2+\frac 32x-1=0$
$x_1=-\frac 23 ,$$x_2=\frac 13 $
∴两个交点的坐标分别是$(-\frac {2}{3},$0)、$ (\frac {1}{3},$0)
∴线段AB的长为1
(3) 由(2)中抛物线顶点P 的坐标为$(- \frac {1}{6},$$- \frac {9}{8} )$
∴△ABP 的面积是$ \frac {1}{2} ×1× \frac {9}{8}=\frac {9}{16}$
10. 已知二次函数 $ y = x^{2}-x - 1 $ 的图像与 $ x $ 轴的一个交点坐标为 $ (m,0) $,则代数式 $ 2m^{2}-2m + 1 $ 的值为
3
.
答案:2018
11. 我们知道,一元二次方程 $ -x^{2}+2x + 3 = 0 $ 的根是二次函数 $ y = -x^{2}+2x + 3 $ 的图像与 $ x $ 轴交点的横坐标:$ x_{1} = -1 $,$ x_{2} = 3 $. 观察图像可知,不等式 $ -x^{2}+2x + 3 > 0 $ 的解集是 $ x $ 轴上方的图像所对应的 $ x $ 的值,即 $ -1 < x < 3 $,不等式 $ -x^{2}+2x + 3 < 0 $ 的解集是 $ x $ 轴下方的图像所对应的 $ x $ 的值,即 $ x > 3 $ 或 $ x < -1 $. 利用二次函数的图像可以求某些一元二次不等式的解集. 再如,不等式 $ -x^{2}+2x + 3 > 2 $ 的解集可以利用函数 $ y = -x^{2}+2x + 3 $ 的图像来求. 它可以看作过点 $ (0,2) $ 且平行于 $ x $ 轴的直线上方的图像所对应的 $ x $ 的值,即 $ 1 - \sqrt{2} < x < 1 + \sqrt{2} $,还可将这个不等式化成 $ -x^{2}+2x + 1 > 0 $,利用函数 $ y = -x^{2}+2x + 1 $ 的图像求解,即 $ x $ 轴上方的图像所对应的 $ x $ 的值.
用上述方法求不等式 $ 2x^{2}+3x - 2 > 0 $ 的解集.

答案:解:如图所示
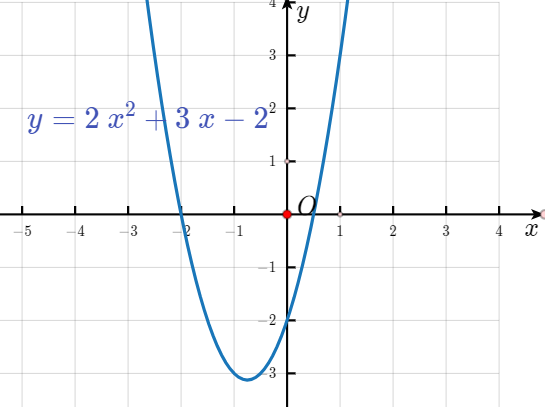
函数$y=2x^2+3x-2$在x轴上方的图像所对应的x值为
x<-2或$x>\frac 12$
∴不等式$2x^2+3x-2>0$的解集为x<-2或$x>\frac 12$