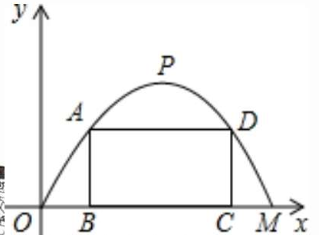
5. 某施工队要修建一条横截面为抛物线形的公路隧道,其高度为6 m,宽度OM 为12 m.现以 O 为原点,OM 所在直线为 x 轴,建立平面直角坐标系(如图).
(1)请写出点 M 及抛物线顶点 P 的坐标.
(2)求这条抛物线相应的函数表达式.
(3)施工队计划在隧道门口搭建一个矩形脚手架 ABCD,使点 A、D 在抛物线上,点 B、C 在地面 OM 上.为了筹备材料,需求出脚手架的三根木杆 AB、AD、DC的长度之和的最大值,请你帮助施工队计算出结果.

答案:解:(1)M(12,0),P(6,6)
(2)∵顶点坐标(6,6)
∴设$y=a(x-6)^2+6(a\neq 0)$
又∵图象经过(0,0)
∴$0=a(0-6)^2+6$
∴$a=-\frac {1}{6}$
∴这条抛物线的函数解析式为$y=-\frac {1}{6}(x-6)^2+6,$
即$y=-\frac {1}{6}x^2+2x.$
(3)设A(x,y)
∴A(x,$-\frac {1}{6}(x-6)^2+6)$
∵四边形ABCD是矩形,
∴$AB=DC=-\frac {1}{6}(x-6)^2+6,$
根据抛物线的轴对称性,可得:OB=CM=x,
∴BC=12-2x,即AD=12-2x,
∴令$L=AB+AD+DC=2[-\frac {1}{6}(x-6)^2+6]+12-2x=-\frac {1}{3}x^2+2x+12$
$=-\frac {1}{3}(x-3)^2+15.$
∴当x=3,L最大值为15
∴AB、AD、DC的长度之和最大值为15米.