27. (10 分)已知抛物线 $C_{1}$ 与 $x$ 轴的一个交点为$(-4,0)$,对称轴所在直线相应的函数表达式为 $x = -1.5$,且该抛物线过点$(-1,6)$。
(1)求抛物线 $C_{1}$ 相应的函数表达式。
(2)求出与抛物线 $C_{1}$ 关于原点对称的抛物线 $C_{2}$ 相应的函数表达式,并在 $C_{1}$ 所在的平面直角坐标系中画出 $C_{2}$ 的图像。
(3)在(2)的条件下,抛物线 $C_{1}$ 与抛物线 $C_{2}$ 相交于 $A$、$B$ 两点(点 $A$ 在点 $B$ 的左侧)。若点 $P$ 在抛物线 $C_{1}$ 上,且位于点 $A$ 和点 $B$ 之间;点 $Q$ 在抛物线 $C_{2}$ 上,也位于点 $A$ 和点 $B$ 之间。当 $PQ // y$ 轴时,求 $PQ$ 的最大值。
答案:解: (1)设抛物线${C}_1$的函数表达式为y= ax²+ bx +c
由题意得,
$\begin{cases}{0=16a-4b+c}\\{-\dfrac {b}{2a}=-1.5}\\{6=a-b+c} \end{cases}$
解得a=-1,b=-3,c=4
所以抛物线${C}_1$的函数表达式为y= -x²- 3x +4
(2)抛物线${C}_2$的图像如图所示,
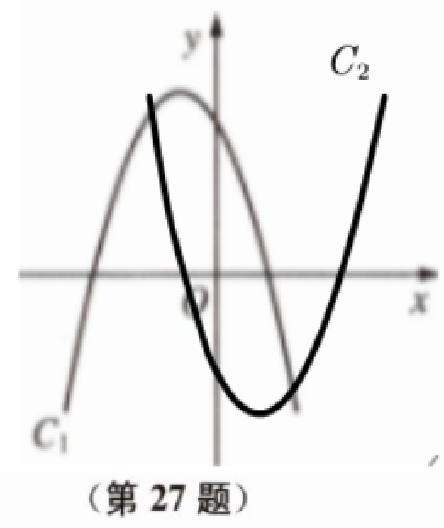
设抛物线${C}_2$的函数表达式为y= dx²+ex+f ,
则抛物线${C}_2$与x轴交点为(4 , 0) ,对称轴所在直线为x = 1.5,
且抛物线过点(1.-6)。
由题意得,
$\begin{cases}{16d+4e+f=0 }\\{-\dfrac {c}{2d}=1.5}\\{d+e+f=-6} \end{cases}$
所以d=1,e=-3,f=-4
抛物线${C}_2$的函数表达式为y=x²-3x-4
(3)由题意得,-x²-3x+4=x²-3x-4,
解得,x=±2
所以点A横坐标为-2 ,点B横坐标为2
设点P的横坐标为t ,则点P坐标为(t,-t² - 3t +4)
因为PQ//y轴,点P的横坐标为t ,
所以点Q的横坐标也为t
因为点Q在抛物线${C}_2$上,
所以点$Q_{坐标} $为(t,t²- 3t- 4)
所以PQ=(-t²-3t+4)- (t²- 3t-4)=-2t²+ 8
因为点P位于点A和点B之间,