2026年伴你学九年级数学下册苏科版第90页解析答案

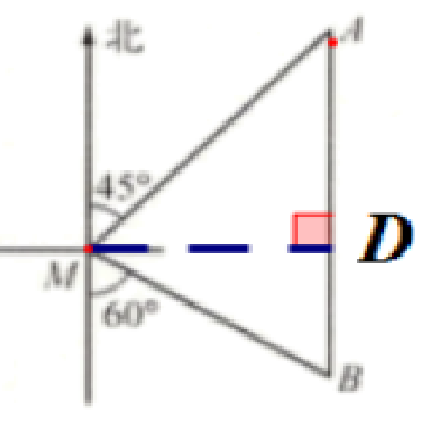
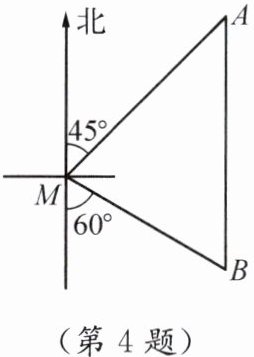
4.如图，一艘渔船位于小岛$M$的北偏东$45^{\circ}$方向、距离小岛$180\ n\ mile$的$A$处，渔船从$A$处沿正南方向航行一段距离后，到达位于小岛南偏东$60^{\circ}$方向的$B$处.
(1)求渔船从$A$处到$B$处的航行过程中与小岛$M$之间的最短距离(用根号表示).
(2)若渔船以$20\ n\ mile/h$的速度从$B$处沿$BM$方向行驶，求渔船从$B$处到达小岛$M$的航行时间.(结果精确到$0.1\ h$;参考数据:$\sqrt{2}\approx 1.41$，$\sqrt{3}\approx 1.73$，$\sqrt{6}\approx 2.45$)

答案：
解：(1)过点M作MD⊥AB ，垂足为点D
$MD= AM · cos 45°= 90\sqrt{2}($海里)
答：渔船从A处到B处的航行过程中与小岛之间的最小距离是$90\sqrt{2}$海里。
(2)因为$MD= 90\sqrt{2}$海里
则$MB=\frac {MD}{cos 30°}= 60\sqrt{6}$
$60\sqrt{6}÷20=3\sqrt{6}≈7.4($时)
答：渔船从B处到达小岛M的航行时间约为7.4时。

1.如图，已知$\triangle ABC$内接于半径为$1$的$\odot O$，$\angle BAC=\theta$($\theta$是锐角)，则$\triangle ABC$的面积的最大值为(

A.$\cos\theta(1 + \cos\theta)$
B.$\cos\theta(1+\sin\theta)$
C.$\sin\theta(1+\sin\theta)$
D.$\sin\theta(1+\cos\theta)$

答案：D

2.如图①，我国传统建筑的大门上常常悬挂着巨大的匾额.如图②，线段$BC$是悬挂在墙壁$AM$上的某块匾额.已知$BC = 1\ m$，$\angle MBC = 37^{\circ}$.从水平地面点$D$处看点$C$的仰角$\angle ADC = 45^{\circ}$，从点$E$处看点$B$的仰角$\angle AEB = 53^{\circ}$，且$DE = 2.4\ m$.(参考数据：$\sin 37^{\circ}\approx\frac{3}{5}$，$\cos 37^{\circ}\approx\frac{4}{5}$，$\tan 37^{\circ}\approx\frac{3}{4}$)
(1)求点$C$到墙壁$AM$的距离；
(2)求匾额悬挂的高度$AB$.

答案：
2. 解： (1)过点C作CF⊥AM，垂足为点F

∴CF=sin∠FBC×BC≈0.6m

答：点C到墙壁AM的距离为0.6m。

(2)过点C作CG⊥AD，垂足为点G

设AB=xm

由(1)知，BF=cos 37°×BC≈0.8m

∵∠AEB= 53°

∴∠ABE=90°-53°= 37°

∴AE= tan 37°×AB=\frac {3}{4}x

DG= AE+ DE- CF=\frac {3}{4}x+ 1.8

∵∠ADC=45°

∴CG= DG

∵CG=AB+ BF

∴x+0.8=\frac {3}{4}x+1.8

答：匾额悬挂高度AB为4m。

解析：

(1)过点$C$作$CF \perp AM$于点$F$，在$ Rt \triangle BCF$中，$\angle CBF = 37^{\circ}$，$BC = 1\ m$，$\sin 37^{\circ} = \frac{CF}{BC}$，$CF = BC · \sin 37^{\circ} \approx 1 × \frac{3}{5} = 0.6\ m$，即点$C$到墙壁$AM$的距离约为$0.6\ m$。
(2)设$AB = x\ m$，在$ Rt \triangle AEB$中，$\angle AEB = 53^{\circ}$，$\tan 53^{\circ} = \frac{AB}{AE}$，$\tan 53^{\circ} = \frac{4}{3}$，$AE = \frac{AB}{\tan 53^{\circ}} = \frac{3}{4}x\ m$。
由(1)知$CF = 0.6\ m$，$\cos 37^{\circ} = \frac{BF}{BC}$，$BF = BC · \cos 37^{\circ} \approx 1 × \frac{4}{5} = 0.8\ m$，$AF = AB + BF = (x + 0.8)\ m$。
在$ Rt \triangle ADC$中，$\angle ADC = 45^{\circ}$，$AD = AF = (x + 0.8)\ m$。
$AD = AE + DE$，$DE = 2.4\ m$，$x + 0.8 = \frac{3}{4}x + 2.4$，解得$x = 4$，即$AB = 4\ m$。