1. 观察下表,并解决问题.

(1) 求$a$、$b$、$c$的值,并在表内空格处填入正确的数.
(2) 根据上面的结果判断:
① 是否存在实数$x$,使二次三项式$ax^{2}+bx + c$的值为 0?若存在,求出这个实数值;若不存在,请说明理由.
② 画出函数$y = ax^{2}+bx + c$的图像示意图,由图像确定:当$x$取什么实数时,$ax^{2}+bx + c>3$?
答案: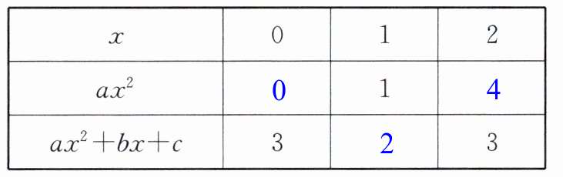
解: (1)当x=0时,ax²+ bx+c=3;
当x= 1时,ax²=1;当x=2时,ax²+bx+c= 3
即$\begin{cases}{c=3 }\\{a=1} \\{4a+2b+c=3} \end{cases} $解得$\begin{cases}{a=1}\\{b=-2}\\{c=3}\end{cases}$
(2)①在x²-2x+3= 0中
∵$b²-4ac=(-2)²-4×1×3= -8\lt 0$
∴不存在实数x使ax²+bx+c=0
②二次函数y= x²-2x+3的图像示意图如下
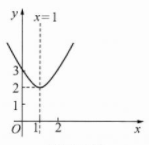
观察图像得出当$x\lt 0$或$x\gt 2$时,$ax²+bx+c\gt 3$