1. 填空。
(1) 可以把一个平行四边形沿高剪开,再拼成一个长方形,这个长方形的面积与原平行四边形的面积(
相等
),它的长与原平行四边形的(
底
)相等,它的(
宽
)与原平行四边形的(
高
)相等。因为长方形的面积等于(
长×宽
),所以,平行四边形的面积等于(
底×高
)。
(2) 一个平行四边形的底是12厘米,面积是156平方厘米,高是(
13
)厘米。
(3)
|平行四边形|底|高|面积|
| |8厘米|6厘米|
48平方厘米
|
| |6分米|
4分米
|24平方分米|
| |
20米
|16米|320平方米|
答案:相等
底
宽
高
长×宽
底×高
13
48平方厘米
4分米
20米
解析:
(1) 把一个平行四边形沿高剪开,再拼成一个长方形,这个长方形的面积与原平行四边形的面积相等,它的长与原平行四边形的底相等,它的宽与原平行四边形的高相等。因为长方形的面积等于长乘宽,所以,平行四边形的面积等于底乘高。
(2) 根据平行四边形面积公式$S = ah$($S$是面积,$a$是底,$h$是高),已知底$a = 12$厘米,面积$S = 156$平方厘米,那么高$h=S÷ a = 156÷12 = 13$厘米。
(3)
当底$a = 8$厘米,高$h = 6$厘米时,面积$S=ah = 8×6 = 48$平方厘米。
当面积$S = 24$平方分米,底$a = 6$分米时,高$h = S÷ a=24÷6 = 4$分米。
当面积$S = 320$平方米,高$h = 16$米时,底$a=S÷ h = 320÷16 = 20$米。
2. 求下面平行四边形的面积。
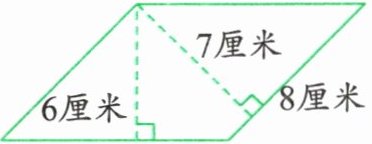

答案:8×7=56(平方厘米)
9×4=36(平方厘米)
3. 用四根木条制成一个长方形木框,长24厘米,宽16厘米。它的周长和面积各是多少?如果把它拉成平行四边形,周长和面积有没有变化?

答案:(24+16)×2=80 (厘米)
24×16=384 (平方厘米)
答:它的周长是80厘米,面积是384平方厘米。拉成平行四边形,周长
没有变化,面积变小。
解析:
长方形木框的周长和面积
周长:
$ C = (长 + 宽) × 2 = (24 + 16) × 2 = 40 × 2 = 80 $(厘米)
面积:
$ S = 长 × 宽 = 24 × 16 = 384 $(平方厘米)
拉成平行四边形后的变化
周长:不变(仍为80厘米)。
面积:变小(平行四边形的高小于原长方形的宽,底不变,面积减小)。